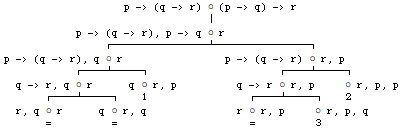Beweren en bewijzen/de zuilen/Zekerheid/4. Nagaan

literatuur ...

Zijn je formules syntactisch correct?

Dat bepaal je aan de hand van een grammatica.

Kloppen de bereiken van quantoren?

Voor predicaatlogica zijn verschillende notaties gebruikelijk. Daarbij kan het bereik van quantoren verschillen. Voor je begint een formule te lezen moet je weten wat in de gebruikte notatie het bereik van de quantoren is. Ook dit volgt natuurlijk weer uit onze Bestand:Grammatica.pdf.

Het bereik maakt verschil! Ga nog eens goed na welke van de formules hieronder logisch equivalent zijn!

∀x:M, HH x → BKB.

(∀x:M, HH x) → BKB.

∃x:M, HH x → BKB.

(∃x:M, HH x) → BKB.

Is een formule een tautologie?

literatuur Van Benthem hoofdstuk 3.2 en 3.4

Dit kun je nagaan door een waarheidstabel te maken (moeilijk, foutgevoelig, arbeidsintensief) of door een proof checker, bijvoorbeeld Coq, te gebruiken. Of je gaat het systematisch na met een doordachte strategie. Een goed voorbeeld van zo'n strategie maakt gebruik van zogenaamde semantische tableaus.

In het boek van Van Benthem wordt de essentie van deze methode uitgelegd in de alinea's ‚Sequent’ en ‚Semantisch tableau’ in hoofdstuk 3.2 en 3.4. Voor wie niet over dat boek beschikt, onderaan deze pagina zullen we een samenvatting geven van hoe je met deze tableaus werkt. Voor wie wel over dat boek beschikt, volgt hier een waarschuwing: In de tweede alinea over notatie staat dat men tableaus kan vereenvoudigen door alleen de dingen op te schrijven die veranderen. Dit maakt de zaak echter erg ondoorzichtig voor jezelf en voor anderen. In responsiecolleges en in het tentamen moet je al je tableaus volledig opschrijven, pas dan zijn ze goed controleerbaar.

Regels voor semantische tableaus (pdf)

• Waarheidstabellen kunnen te groot worden, te groot om ze nog te overzien of te groot om ze überhaupt te kunnen opschrijven. Daarom kan het handiger zijn te beredeneren of ergens een 0 kan staan. Dat is het idee van tableaus: systematisch nagaan of er een tegenvoorbeeld is, een combinatie van waarheidswaarden van de proposities die de formule onwaar maakt.
• Men schrijft de formule op en breekt ze dan langs haar constructieboom af in steeds kleinere stukjes. Bij elk voegteken horen twee regels die men schematisch moet toepassen.
• Bij elke stap wordt één voegteken weggewerkt. Na eindig veel stappen wordt zo duidelijk of er een tegenvoorbeeld is.
• Van Benthem schrijft in zijn boek helaas de tableaus zelden volledig op. Hij schrijft alleen de formules op die veranderen en laat de rest weg. (Opmerking over notatie na voorbeeld 3.5). Dat is gevaarlijk. Je raakt makkelijk het overzicht kwijt als je niet heel goed weet wat je doet. Schrijf liever de ontbrekende formules in je boek erbij!

Tableaus

Sequenten

Voordat we kunnen aangeven hoe we bij een gegeven vraag een semantisch tableau kunnen maken, moeten we eerst het begrip sequent introduceren. Een sequent is een rijtje

Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \phi_1,\phi_2,\dots,\phi_n \circ \psi_1,\psi_2,\dots,\psi_m}

waarbij Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \phi_1,\phi_2,\dots,\phi_n} en Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \psi_1,\psi_2,\dots,\psi_m} twee rijtjes met formules zijn. Een tegenvoorbeeld van zo'n sequent is een waardering Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V} met voor alle i=1,...,n: Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V(\phi_i)=1} en voor alle j=1,...,m: Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V(\psi_j)=0} . Met andere woorden, een waardering is een tegenvoorbeeld van zo'n sequent als alle formules links van de Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \circ} WAAR zijn en alle formules rechts van de Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \circ} ONWAAR zijn.

Tableaus hebben de fijne eigenschap dat ze helpen om op een systematische wijze een tegenvoorbeeld van een sequent te kunnen zoeken. Maar normaal gesproken kom je in de praktijk geen sequenten tegen, maar beweringen als

Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p \rightarrow (q \rightarrow r) \vDash (p \rightarrow q) \rightarrow r}

In dit geval is het overigens een onjuiste bewering. Dus moeten we een tegenvoorbeeld kunnen vinden dat aantoont dat Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (p \rightarrow q) \rightarrow r} geen logisch gevolg is van Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p \rightarrow (q \rightarrow r)} . Om van deze bewering een sequent te maken, moeten we onszelf de volgende vraag stellen: wat betekent het om een tegenvoorbeeld te hebben voor een Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi \vDash \Psi} bewering? (Als hier hoofdletters Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi} en Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Psi} worden gebruikt, dan staat dat voor een, mogelijk leeg, rijtje formules.) Gezien de definitie van logisch gevolg is de enige manier hiervoor dat we een waardering Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V} vinden met Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V(\Phi)=1} en Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V(\Psi)=0} . Maar dat komt precies overeen met de sequent Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi \circ \Psi} . Dus als we een tegenvoorbeeld voor onze bewering willen vinden, moeten we een tableau maken bij de sequent

Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p \rightarrow (q \rightarrow r) \circ (p \rightarrow q) \rightarrow r}

En eigenlijk is hiermee het moeilijkste werk gedaan! Vanaf nu is het een kwestie van consequent de reductieregels toepassen.

Reductieregels

De reductieregels staan hierboven allemaal genoemd in het plaatje. Zoals je ziet zijn er voor elke logische operator twee regels: een regel voor als die operator aan de linkerkant van Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \circ} staat en een regel voor als die operator aan de rechterkant staat. Het idee is dat je vanuit de startsequent in elke stap precies één reductieregel toepast om een of twee nieuwe sequenten te krijgen. In het bijzonder heeft elk van die nieuwe sequenten precies één operator minder. Dus als je dit gaat herhalen, zul je altijd in een eindig aantal stappen op sequenten komen waarin geen operatoren meer zitten en waarop dus ook geen reductieregels meer toegepast kunnen worden. Als je dit voor alle mogelijke vertakkingen doet krijg je uiteindelijk het hele tableau. Door in dat tableau te kijken of er open takken zijn of juist alleen maar gesloten takken kun je bepalen of de bewering klopt of niet. Elke open tak geeft je namelijk precies één type van tegenvoorbeeld. Dus als de bewering onjuist is, moet je dus ergens een open tak hebben gevonden. En als de bewering wel waar is, moet je dus alleen maar gesloten takken hebben gevonden. Merk op dat het soms niet nodig is om het hele tableau af te maken! Als je op zoek bent naar een tegenvoorbeeld is het voldoende om één open tak te vinden. Heb je die eenmaal gevonden, kun je dus stoppen. Wordt er echter gevraagd om alle tegenvoorbeelden of juist om te bewijzen dat de bewering wel klopt, dan moet je wel het hele tableau afmaken.

Als je tableau meer dan een formule, gescheiden door komma's, bevat, kun je een willekeurige formule kiezen waarop je verder werkt. Sommige keuzes leiden sneller tot resultaat dan andere, maar voor de waarheid maakt de keuze niet uit. Binnen een formule moet je logischerwijs de syntaxboom van de formule volgen, d.w.z. op de zwakst bindende operator werken.

Gesloten takken

We noemen een tak gesloten als er GEEN tegenvoorbeeld meer kan worden gevonden in die tak. Dat is precies als de laatste sequent in die tak van de volgende vorm is:

Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi, f \circ \Psi, f}

Of in woorden: als er aan de linkerkant precies dezelfde formule Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} staat als aan de rechterkant. Immers, een tegenvoorbeeld is een waardering die alle formules links waar maakt en alle formules rechts onwaar. Maar als een formule aan beide kanten staat, moet die dus tegelijk waar en onwaar zijn en dat is onmogelijk in onze tweewaardige logica. Ook als er nog operatoren staan in zo'n sequent die je kunt reduceren, heeft dat geen nut. Vandaar dat je dan ook meteen mag stoppen met het uitwerken van zo'n tak. (Hij heet ook niet voor niets gesloten.)

Open takken

Bij open takken kun je juist WEL een tegenvoorbeeld vinden. Een tak heet open als er in de laatste sequent geen reductieregels meer kunt toepassen en er geen formules zijn die links en rechts voorkomen. In het bijzonder ben je dan uitgekomen op een sequent van de volgende vorm

Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_1,a_2,\dots,a_n \circ b_1,b_2,\dots,b_m}

waarbij alle Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a_i} en Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b_j} atomen zijn. Het tegenvoorbeeld uit die open tak wordt gevormd door de valuatie Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V} met Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V(a_i)=1} en Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V(b_j)=0} (voor alle i en j) te nemen. Merk op dat het kan zijn dat niet alle atomen uit de bewering in dit sequent staan. Wat moet (of mag) de waarde van Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle V} op die atomen dan zijn?

Reductieregels (vervolg)

Moet je nu de reductieregels uit het hoofd leren? Nee, je moet ze zien te begrijpen. Alle regels zijn gebaseerd op de al bekende waarheidstabellen samen met de vraag wat het betekent dat een bepaalde operator ofwel aan de linker- ofwel aan de rechterkant staat. Neem bijvoorbeeld de sequent Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi \circ \Psi, a \and b} . De Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a \and b} staat aan de rechterkant, dus de formule Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a \and b} moet onwaar zijn. Maar wanneer is een Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \and} -formule onwaar? Als Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} onwaar is of als Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b} onwaar is. Dat levert dus twee nieuwe takken met daarin de sequenten Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi \circ \Psi, a} en Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi \circ \Psi, b} . (Bedenk zelf waarom het niet nodig is om ook een derde tak te maken met Parsen mislukt (MathML met SVG- of PNG-terugval (aanbevolen voor moderne browsers en toegankelijkheidshulpmiddelen): Ongeldig antwoord ("Math extension cannot connect to Restbase.") van server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Phi \circ \Psi, a, b} .) Bij de andere operatoren werkt het net zo: staat de operator links, dan moet je kijken welke deelformules waar danwel onwaar moeten zijn om de hele formule waar te laten zijn. De ware deelformules komen aan de linkerkant te staan, de onware rechts. En stond de operator aan de rechterkant, dan moet je bekijken welke deelformules waar of onwaar moeten zijn om de totale formule onwaar te laten zijn.

Voorbeeld

Vergelijk dit eventueel met voorbeeld 3.8 uit het boek van Van Benthem:

De gesloten takken zijn aangegeven met een ‚=’. De open takken met een nummer 1, 2 of 3. Deze drie open takken leggen de waarderingen dus alsvolgt vast:

• V1(p)=0, V1(q)=1, V1(r)=0
• V2(p)=0, V2(r)=0
• V3(p)=0, V3(q)=0, V3(r)=0

Hoeveel verschillende tegenvoorbeelden bestaan er dus die de bewering waar we mee begonnen waren ontkrachten?