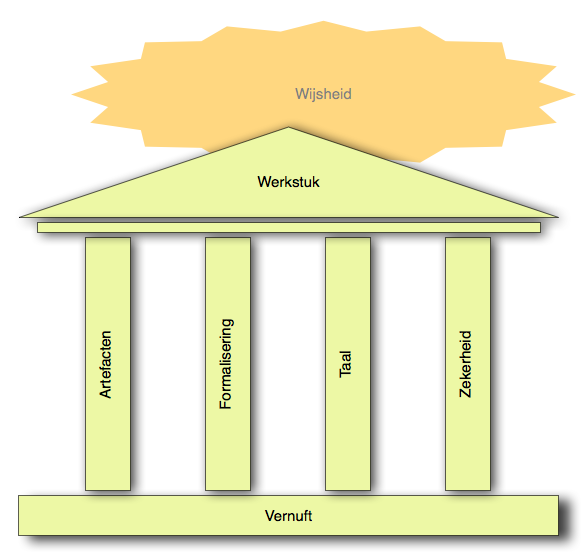
Beweren en bewijzen/de aanpak/vier zuilen

Onzekerheid is griezelig. Maar men kan leren, zelf zekerheid in zijn hoofd te scheppen. Men kan leren een griezelig probleem - lang voor men een oplossing ziet - in deelproblemen op te splitsen, die elk voor zich al stukken minder griezelig zijn. Men kan leren exacte en ondubbelzinnige beweringen te formuleren waarmee het wezenlijke van het onwezenlijke wordt gescheiden. Men kan dingen bewijzen en dan goed nagaan wat men eigenlijk bewezen heeft en wat dat zegt. Kortom: men kan leren, macht over de onzekerheid te krijgen: door middel van scherp redeneren op het hoogste niveau, door middel van logica en wiskunde.

Maar hoe? Onze leerdoelen verbinden dit redeneren op het hoogste niveau met het vraagstuk van correctheid van gemaakte dingen.

Vier inhoudelijk orthogonale cursussen die ook los van elkaar gevolgd zouden kunnen worden:
Artefacten	Formalisering	Taal	Zekerheid
Mensen maken →artefacten omdat ze dingen willen hebben die doen wat ze moeten doen. De informatica en informatiekunde richt zich daartoe voornamelijk op artefacten waarbij informatieverwerking een grote rol speelt. Of zulke artefacten doen wat ze moeten doen kan alleen worden bepaald als men ook de omgeving begrijpt waarin ze moeten functioneren. De informatica heeft gedurende de afgelopen decennia talloze theorieën, methoden, talen en gereedschappen ontwikkeld die helpen bij het ontwerpen, realiseren en verifiëren van zulke artefacten. De cursussen in het informatica- en informatiekundecurriculum besteden meestal aandacht aan enkele deelvragen. Hier geven we het overzicht: waar gaat het eigenlijk om? Wat wil men eigenlijk met zo'n artefact precies bereiken? Deze vraag kan al een →gemeen probleem zijn. En dan moet men het ding ook nog bedenken en maken. En zichzelf en anderen vervolgens overtuigen dat het goed is. Bij al deze stappen maakt men keuzes en komt men vaak op eerdere keuzes terug. Het is een moeizaam proces, dat poogt zekerheid te scheppen in een gebied vol onzekerheden. De hoofdstukken 1. Het Rationaliteitsvierkant 2. Focus 3. Specificaties 4. Structuur 5. Decompositie 6. Domeintheorie 7. Hiërarchische decompositie 8. Standaardisatie richten zich daarom vooral op omgaan met onzekerheid. Professionele informatici en informatiekundigen moeten daar goed in zijn.	We willen betrouwbaar redeneren over vraagstukken omtrent de fysieke realiteit. Absolute zekerheid dat een redenering klopt biedt de wiskunde, maar die gaat niet over de fysieke realiteit, hooguit over een wiskundig model van een aspect ervan. Hoe hangen de eigenschappen van →dingen samen met zulke wiskundige modellen? Wiskundige objecten (bijvoorbeeld getallen als onderdeel van een model van de realiteit) als ook redeneringen erover moeten we opschrijven om ze te kunnen communiceren en controleren. Zowel de beschrijving van wiskundige objecten als de beschrijving van redeneringen kunnen, maar hoeven niet, in een formele taal gesteld zijn. Sommige cursussen van de opleiding gaan óf over een stuk wiskunde óf over een stuk realiteit. Hier, in de hoofdstukken 1. Vier werelden 2. Precisie 3. Domeinmodel 4. Correctheidsstelling 5. Systematisch vertalen 6. Tijd 7. Vereenvoudigingen 8. Parametrisatie wordt uitgelegd hoe deze verschillende werelden in elkaar zitten, wat ze met elkaar te maken hebben en hoe je ermee omgaat.	De hoofdstukken 1. Beweren is moeilijk 2. Logica 3. Syntax en semantiek latex 4. Typering 5. Definities Grondwet 6. Tijdslogica bieden houvast bij het ontwerpen en verifiëren van →artefacten: hier leer je een formele taal die geschikt is voor de specificatie van eigenschappen van artefacten en hun onderdelen. Deze taal is voor mensen die ze beheersen redelijk leesbaar (i.t.t. bijvoorbeeld de nullen en enen van een machinetaal) en geschikt voor het gestructureerd specificeren van grotere systemen. Bij deze taal hoort een bewijsassistent. dat is een computerprogramma dat beweringen op syntactische correctheid en juiste typering controleert en helpt bij het maken van correctheidsbewijzen. Voor deze doelen zijn honderden verschillende talen, notaties en gereedschappen in gebruik, elk met haar eigen voor- en nadelen. Wij kiezen een taal die universeel bekend en onomstreden is, een taal die misschien wat minder makkelijk "werkt" dan andere talen, maar waarin men het beste kan zien waar het eigenlijk om gaat: formele logica. Logica werkt totaal anders dan een programmeertaal. In de logica zeg je wat het geval is. In een programmeertaal instrueer je een computer wat zij achtereenvolgens moet doen. Als je logica wilt gebruiken doe je er goed aan, te vergeten wat je bij programmeertalen gewend bent.	Stel, je hebt je kennis van de wereld onderverdeeld in een aantal beweringen, waarvan je zeker bent dat ze waar zijn. Laten we deze beweringen je aannames noemen. Je trekt uit deze aannames een conclusie. Hoe krijg je zekerheid dat deze conclusie waar is? In de hoofdstukken 1. Overtuigen 2. Stelling en bewijs 3. Waarheid 4. Nagaan Oefenstellingen 5. Natuurlijke deductie bewijsstrategie deductieschema latex predikaatlogica stellingen propositielogica stellingen P of niet P 6. Wiskunde oefenstellingen 7. Bewijsassistenten 8. Hulpstellingen leer je wat dit eigenlijk betekent, hoe het kan zonder dat je in complexiteit verzuipt en hoe een computer daarbij kan helpen.
Na voltooiing van deze cursus kun je...
een gegeven of nog te bedenken artefact systematisch hiërarchisch onderverdelen, beredeneren dat bepaalde eigenschappen van het artefact waar gemaakt worden door de eigenschappen van zijn gezamenlijke onderdelen, idealiter gewenste eigenschappen op een verantwoorde manier afzwakken tot eigenschappen die realiter waar gemaakt kunnen worden, aangeven wat de rol van formalismen en formele methoden in dit proces is, een exemplarische formele methode en de bijbehorende bewijsassistent (in casu Coq) ervoor gebruiken, een verslag over de correctheid van het artefact maken waarin de resultaten van formele methoden voor leken toegankelijk gepresenteerd worden.	uit een vaag en niet afgebakend reëel probleem (in casu een correctheidsvraagstuk over een artefact) een deelprobleem destilleren dat zich formeel bewijzen laat, een fragment van de realiteit onder een relevant aspect formeel modelleren (in casu m.b.v. propositie- en predicaatlogica), verantwoorden dat het model werkelijk slaat op de fysieke realiteit, met behulp van een exemplarische formele methode en de bijbehorende bewijsassistent (in casu Coq) een volledig bewijs leveren, aangeven wat de valkuilen zijn bij het toepassen van formele methoden op vage problemen uit de realiteit en hoe men daarmee systematisch omgaat.	een exemplarische specificatie- en een verificatietaal (in casu Coq en natuurlijke deductie) toepassen op middelgrote correctheidsvraagstukken, conform een formele grammatica de syntaxboom van teksten uit een formele taal construeren en langs deze boom de betekenis van de tekst afleiden, middelgrote specificaties correct in deze taal opschrijven en wel zo dat ze ook voor mensen leesbaar en begrijpelijk zijn, een bewijsassistent (in casu Coq) gebruiken voor correctheidsbewijzen.	beweringen opschrijven in propositie- en predicaatlogica, vraagstukken als stellingen met aannames en conclusies formuleren in logica, stellingen op een gestructureerde manier in natuurlijke taal bewijzen, in het geval van propositielogica: waarheid aantonen m.b.v. waarheidstabellen en semantische tableaus, stellingen bewijzen met natuurlijke deductie met potlood en papier en met behulp van een bewijsassistent (in casu Coq).
Een filosofisch verantwoord verhaal met oplopende complexiteit:
1. Rationaliteit Hoe kunnen we met ons verstand greep krijgen op de wereld om ons heen? Om dit te onderzoeken beperken we ons in eerste instantie tot de correctheid van →artefacten, d.w.z. tot de vraag hoe we zeker kunnen zijn dat door ons en anderen gemaakte dingen doen wat ze geacht zijn te doen. 2. Modellen Redeneren we eigenlijk over de fysieke realiteit om ons heen of redeneren we over een model van de realiteit, dat we in ons hoofd hebben? En als we over het redeneren redeneren? Formele logica is een model van het redeneren. 3. Model en realiteit Binnen de wereld van de wiskunde kunnen we prachtige modellen bouwen en erover redeneren. We kunnen computers gebruiken om ons te helpen bij het redeneren. We kunnen computers zelfs beslissingen laten nemen en uitvoeren. Maar waar slaat dit op? Hoe kunnen we zeker zijn dat het redeneren over modellen iets zegt over de realiteit? En hoe kunnen we zeker zijn dat het redeneren over (modellen van) het redeneren iets zegt over het redeneren? 4. Correctheid Een →artefact noemen we correct, als het doet wat het moet doen. Een reeks van tekens noemen we een correcte (niet noodzakelijk ware) formule, als ze in de desbetreffende taal iets betekent. Een redenering noemen we correct, als ze sluitend is. Wat betekent dit allemaal precies? 5. Methoden Begrijpen waar het om gaat is niet genoeg, we moeten het ook doen: een gegeven ingewikkeld →artefact opsplitsen in onderdelen, een nog niet bestaand artefact ontwerpen, een ingewikkelde bewering correct opschrijven in de gewenste taal, een correcte redenering in elkaar zetten. Professionals doen zoiets op een systematische manier. In de wereld van de IT wordt een groot aantal methoden gepropageerd, en sommige leer je in deze opleiding kennen. Hier richten we ons op methoden die zo algemeen en fundamenteel zijn, dat je ze als leidraad kunt gebruiken bij het leren van andere talen en methoden. 6. Theorie De exacte wetenschappen zijn eeuwenlang bezig om theorieën te ontwikkelen, die ons helpen bij het redeneren over bepaalde soorten vragen en bepaalde aspecten van de wereld. Hoe kunnen we daarvan gebruik maken? Bij elk toepassingsgebied van de IT horen domeinspecifieke theorieën. Als voorbeeld beschouwen we onder andere real-timesystemen en een eenvoudig stukje theorie van de tijd. 7. Complexiteit Alles wordt al gauw zo complex, dat we moeite hebben het te overzien: de dingen zelf, de beschrijvingen ervan en de redeneringen erover. Hoe gaan we professioneel om met zulke complexiteit? 8. Generalisering Een academicus lost niet alleen het ene probleem na het andere op, hij (m/v) staat bij elk nieuw resultaat ook stil bij de vraag: kan ik dit generaliseren, zodat ik er iets aan heb bij een volgend probleem dat er enigszins op lijkt? Hoe gaat dit in zijn werk?
Het Cartesisch product: vier parallelle cursussen in één:

De docenten willen jullie helpen experts te worden op het gebied van onzekerheid. Maar dat kun je alleen leren als je ook af en toe aan onzekerheid bloot staat. Bijvoorbeeld door practicumopdrachten uit te voeren waarvan niemand al in het begin de goede oplossing kent. Als je dat niet gewend bent, is dat griezelig, dat weten we. Maar nu is de tijd, eraan gewend te raken.

Waarheen? Als je deze cursus voltooid hebt, heb je twee proeven van bekwaamheid geleverd:

Werkstuk 

Je hebt samen met een paar medestudenten een werkstuk geschreven waarin je laat zien dat je op professioneel niveau iets kunt doen dat tot de kern van de informatica en informatiekunde hoort.

Theorie 

Je hebt in een aantal tentamens aangetoond dat je de nodige theoretische kennis hebt en kunt toepassen. Deze tentamens doe je in een bepaalde volgorde, volgens een bepaald rooster. Elk tentamen is de afsluiting van één van de hoofdstukken waarin de stof onderverdeeld is.

Hoe het allemaal in zijn werk gaat staat beschreven in de opzet.