Taxonomy/1. Quality/01. Rationality
"Beyond reasonable doubt" – what does that mean?
Inhoud
Certainty
There are four ways to be sure that something is the case. The most reliable one does not guarantee anything about reality. The other three can be misleading. So we better be careful.
Deduction
We deduce (derive) conclusions from assumptions. Such a derivation is valid if it follows the rules of →deduction. Such rules have been established (by means of induction) during the last two thousand years. They ensure that if some assumptions hold in reality, a valid conclusion from these assumptions will also hold in reality. →formal rules and techniques of deduction have been developed to highest standards during the last two centuries. Deduction provides certainty – but not about the physical world, only about statements (descriptions), be it in natural, be it in a formal language. In the best case, these statements have well-defined semantics in the world of mathematical objects.
Induction
If we want to be sure that our assumptions about physical phenomena hold indeed we try to get evidence by repeated observations: →induction justifies statements about reality. During the last centuries experimental science has developed a discipline of induction. About simple things like planets, billard balls, lenses, or transistors, induction provides reliable knowledge. Applied to complex things like computers, it can be misleading. Ill-understood induction leads to superstition, as in the case of Skinner's pigeons [1].
Insight
In some lucky cases →insight – acute observation – makes us understand immediately, without further explanation or reasoning, how an artefact works, what a formula means, or that a theorem holds. "ηὕρηκα!" Insight can be misleading. Insight can also be trained.
Faith
| "An etwas glauben heißt, sich in jeder Lage so verhalten, wie man sich verhalten muss, wenn es das, woran man glaubt, wirklich gibt." – Carl Friedrich von Weizsäcker: Zeit und Wissen |
| "Glauben heißt immer: Dazu entschließe ich mich, darauf stelle ich meine Existenz." – Werner Heisenberg: [[]] |
When we don't have the time, motivation, knowledge, or means to find out whether something really is the case, we can nevertheless →faithfully believe it. Civil engineers, for example, have faith that the laws of nature hold. Programmers have faith that their programs are compiled and executed correctly. Otherwise they couldn't start their work. When we buy a product from a →provider we consider as reliable, we have faith that it meets its specification. Believing something, however, does not guarantee it is true, as thousands of millions of people show who believe that Windows is the best operating system. Mathematics has established a discipline to deal with belief: in "axioms" and "assumptions" belief is explicified.
Rationality attempts careful combination of deduction, induction and insight, getting rid of unjustified belief. However, it is impossible to get rid of all belief. Most mathematicians still stress the intuitive appeal or usefulness of their axioms, trying to justify their beliefs.
The Rationality Square: reasoning applied to physical reality
Objects and descriptions
We want certainty about things. Deduction is the most powerful means to obtain certainty, but deduction is applied to statements, to descriptions of things, not to things themselves. Philosophy has taught us to distinguish carefully between objects and their descriptions. Anne is a four-letter word. Anne has a baby. But Anne is not a four-letter word that has a baby. We have learned to use quotes for disambiguation: "Anne" has four letters, while Anne has a baby.
A note for software engineers: A program, viz. a piece of software can be seen as both, a description, which can be subject to reasoning, and a piece of physical reality (magnetism) inside the machine that executes it. Software engineers tend to identify these two, but they live at different levels. (Similarly, the Constitution is a set of rules that prescribe how people should behave, and it is a physical object that one can buy or study in an archive.)
We need induction (possibly in combination with deduction) to relate things to their descriptions.
In the Rationality Square, physical reality is represented at the bottom, below its description. Represented, as it is difficult to include real things in a diagram. We mean a thing, but we can only draw a picture or write some hints to indicate what we mean. In any case, at the top of the Rationality Square, we mean descriptions, not the objects described.
| descriptions: language, reasoning, statements, formulae |
| things and phenomena: physical reality, observation |
Structure and properties
Science uses mathematics to establish valid relations between the →structure of →things and their →properties. To understand a complex object we impose structure on it. We reason about structure to understand why something has its properties, how it "works", and how it can be made. Structure, however, is a subjective, conceptual idea, not an objective property of the object itself. Under different →views, the same thing can be considered to have different structures. An example of imposing structure is to understand a lump of matter as a canon pointed in a certain direction, filled with a certain amount of gun-powder and a ball of a certain weight. Someone from a culture where canons, ballistics, and gun-powder are unknown will not recognise this.
Simple examples of an object’s properties are its weight, speed or colour. An interesting property of the structure mentioned above is whether its ball will hit a certain target. In the context of information technology one is mainly interested in complex, dynamic properties like ‘controlling a nuclear reactor’s temperature’ or ‘navigating an aeroplane’. In the context of classical software engineering, a typical property is the input-output relation of a program.
The left half of the Rationality Square deals with structure, the right half with properties.
|
|
Corner stones
Structure vs. properties, reality vs. mathematics - this gives rise to the corner stones of what we will call the Rationality Square.
| description of structure | description of properties |
| thing: an object on physical reality | properties in physical reality |
This square is common to all exact sciences and engineering disciplines, as a few examples may illustrate. It can be used to describe research questions, design problems, and verification problems. When you explore the examples below, please follow the numbering 1., 2., 3., 4.
- Chemistry
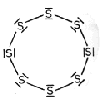
2. Structural formula of flowers of sulphur.
It took centuries of research to find out that the properties of that mineral are determined by this simple structure. |
4. Colour:
#FFFF66 This is a number of a colour in the RGB-language. The languages is so simple because experience has shown that three colour components in 256 intensities suffice to give a close enough description of most colours that human eyes can see.
|
| 3. Certain molecules, too small to be seen. But from the structural formula their geometric shape can be derived. Here, a pencil drawing must give an idea of what it "looks" like. It absorbs light of certain wave lengths. | 1. "Flowers of sulphur"
This mineral has a special colour. But why? |
- Celestial mechanics
| 4. Natural science discovered how the celestial execution mechanism works. If someone gives pieces of matter a certain impulse, Kepler's laws ensure that they circulate around the sun in the right way. What God did can be described by a handful of constants about the distance and speed of the planets. | 3. When astronomy became a science the movements of planets were described in such a way that their future positions could be predicted with high accuracy. |
|
1. In the beginning God created the heaven and the earth... he made the stars also. And God set them in the firmament of the heaven. – Essentially, he made huge lumps of matter circulate around each other. The result is too big to be depicted here. |
2. When homo sapiens started to think, certain periodicies in the movement of stars were observed. Night sky had the property that stars showed repetitive behaviour. |
- Planetarium
3. The celestial execution mechanism, which follows the laws of Newton for just one singe value of the gravitation constant, is unsuitable for living-room usage. Eise Eisinga used tooth wheels instead. Tooth wheels can be used to calculate fractions of integers, but a wheel with six or less teeth will not work properly. He had to solve two design problems:
|
2. The properties should be exactly the same as those of the real planets, with the size of the orbits reduced by a certain factor and the diameter of the planets reduced by another factor. The formal description could easily be derived from the astronomical one by replacing some parameters. |
| 4. The mechanism of the planetarium is hidden in the attic above the living room, where it moves planets that hang from the ceiling. | 1. Around 1770 Eise Eisinga wanted a scale model of the solar system in his living room. It should mimic the movement of planets in real time. |
- Biology
1. The DNA sequence of Quinten Quist
TAACCCTAACCCTAACCCTAACCCTAACCCTAACC CTAACC etc. etc. (The full description of this structure is too large to be included here.) How and to which end it was →constructed is described in detail in Harry Mulisch's book The Discovery of Heaven. Quinten's DNA and education scheme was designed because a specimen of homo sapiens with very special →properties was needed. But this copy of the Rationality Square is not about these properties. It is drawn from another →view and is only about the eye colour. |
4. Eye colour:
#CCCCFF |
| 2. Quinten Quist, the hero of The Discovery of Heaven.
As Quinten no longer lives on earth, we cannot do more than give a picture (a →view) of an actor who played him (a →model). |
3. The colour of Quinten's eyes.
Was this unusual colour intended when Quinten's DNA was designed? Or is it just a side effect of the design? |
- Music
| 3. After Bach had failed to implement the specification at first, he chose for rational →development and, some months later, came up with a complete structural description of not only the specified fugue but a larger composition that satisfied a number of similar specifications. | 1. Frederick the Great gave a precise, unambiguous specification: "A fugue in six voices about this theme:" |
| 2. Joh. Seb. Bach tried to implement the specification but did not succeed then and there. | 4. The properties Frederick the Great had in mind. But note that this →artefact has more properties. (mp3 to be included here) |
Relations
Physical things and mathematical theories must be made to fit. That means that the following relations between the corner stones have to be established carefully:
| description of structure | does every thing with this structure have the described properties? | description of properties |
| does the thing have the described structure? | does the thing have the described properties? | are the properties described correctly? |
| thing: an object on physical reality | does the thing have the meant properties? | properties in physical reality |
Verification
When these relations are defined, how can we convince ourselves that, in a particular case, they hold? Deduction is only applicable in the mathematical world. If the problem is complex, we would like to deal with as much complexity as possible within the mathematical world, where also computerised tools can be used to support reasoning. Then, ideally, the transition between the two worlds can be verified by insight.
| description of structure | deduction, possibly supported by tools | description of properties |
| insight, induction, or, in the case of artefacts, a controlled construction process | insight or induction | |
| thing: an object on physical reality | does the thing really have these properties? | properties in physical reality |
- Flowers of sulphur
- The proof that the structural formula of flower of sulphur gives rise to the specified colour will include chemical knowledge about S8, knowledge about our eyes, and follow this line: the absorption spectrum of sulphur is 4000 to 5500 Ångstroms or 400 to 550 nm. This falls in the violet, blue, and green regions of visible light. This is the light that is absorbed. What is left over, and thus can reach our eyes, is the yellow, orange, and red wavelengths. The mix of these remaining wavelengths is such that the effect on our eyes and brain is similar to that of #FFFF66 on an RGB-display.
- Planetarium
- That Eise Eisinga's planetarium does what it is supposed to do can be established in two ways.
- A correctness proof would ensure that the numbers of teeth of the tooth wheels are such that they compute the right speeds. Such a proof would involve knowledge about all wheels and axes.
- But in this case the planetarium can also be tested. Without counting all teeth we can conclude from the blueprint the simple fact that all movements must have constant speed by construction (all gears are circular). Sitting in the living room, one can determine the actual speed with a few measurements. If these are correct, they will be in future (with respect to the precision of the measurements).
- Eye colour
- The proof that this sequence of DNA gives rise to this specific blue will be similar to that of the colour of flowers of sulphur but will have to follow the whole line of protein synthesis and require a huge amount of biological knowledge.
- Musical Offering
- Music theory knows strict criteria for what a fugue is and what not, and the Ricercar a 6 has been checked against them by generations of music theorists. That it is a fugue about the required theme can easily be seen and heard.