Overleg:Onderzoeksmethoden 2/het werk/2012-13/Group 4

Data analysis

Choice of best classification algorithm

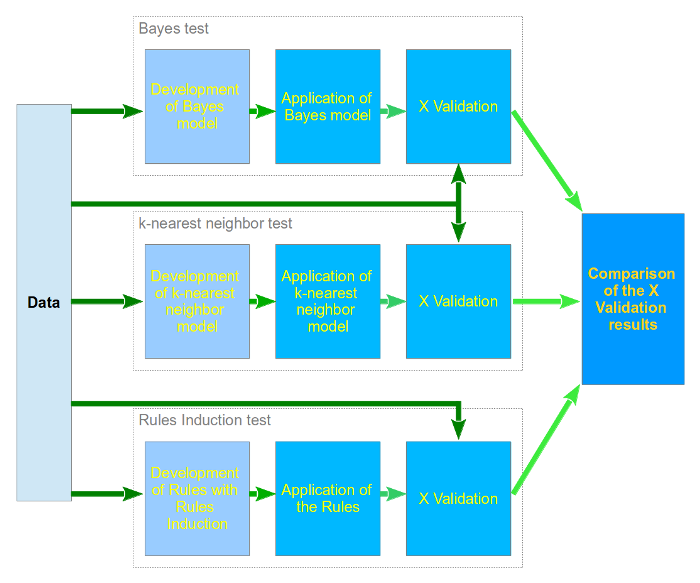
We compared the algorithms Bayes, k-NN and Rules Induction because they fit our dataset very well, as described in the algorithm descriptions below.

Description of algorithms

Ik kan met mijn 384 kbit-verbinding helaas niet rapidminer via ssh openen en het downloaden duurt ook verschrikkelijk lang. Ik zal morgen bij iemand anders even kijken of ik het daar kan opnenen om te kijken welke instellingen ik voor de algoritmes gebruikt heb. Als iemand tijd heeft, mag die als in het algemeen opschrijven hoe de drie algoritmes werken.
Patrick Schileffski → Onderzoeksmethoden 2	Remove this comment when resolved!

Naive Bayes

Naive Bayes (will be referenced as Bayes from now on) also works up to its name. This classification function works naive in such a sense, that it looks at all attributes of an object separately: it does not take dependencies between attributes in consideration. This means that for all attributes the function calculates the probability that this attribute belongs to a certain classification. After this has been done for all attributes, the total chance for the different classifications are calculated, and the classification with the highest chance is assigned.

For our project this suits very well, because all attributes among each other are independent. All attributes may contribute to the classification as much as the other attributes.

k-NN

k-NN stands for k Nearest Neighbor, which pretty much basically describes what this classification function does. The function maps all objects to a multidimensional space (as much dimensions as there are properties), and simply assigns the classification that the majority of neighbors on all dimensions have. So the function, for each dimension, checks what classification the neighbor (so other objects with known classifications) objects have, calculates the classification that is most given to all these neighbors, and assigns this value to the object that is being classified.

The k in this function is the amount of nearest neighbors that are checked. If this value is for instance 3, then 3 neighbors will be checked on their classification.

This function is particularly useful in our research as all theses have a known classification. This means that all objects in the function can be mapped to all other objects, as the neighbor objects always have a classification available.

Rule Induction

The algorithm for Rule Induction that we used is a propositional rule learner named RIPPER. This algoritm starts with less prevalent classes and iteratively grows and prunes rules until there are no positive examples left or the error rate is greater than 50%. When growing, rules are added until the rule is perfect. The procedure tries every possible value of each attribute and selects the condition with the highest information gain (the amount that makes sure as much attributes as possible can be correctly assigned).

This works well with our dataset because it can work good on nominal values, and there is only a small amount of different classifications possible, which should keep the tree relatively small.

Description of evaluation

Results

All the three algorithms needed at most several minutes to classify the 74 theses with 633 attributes. So we think the efficiency of the three algorithms is at least sufficient and we compare only the accuracy of the three algorithms:

Bayes test

Confusion matrix

True	Computer Science	Information Science
Computer Science	2835	235
Information Science	15	2540

accuracy: 95.56% +/- 0.73%

k-NN test

Confusion matrix

True	Computer Science	Information Science
Computer Science	2838	22
Information Science	12	2753

accuracy: 99.40% +/- 0.66%

Rules Induction test

Confusion matrix

True	Computer Science	Information Science
Computer Science	2833	12
Information Science	17	2763

accuracy: 99.48% +/- 0.65%

Chosen algorithm

We have chosen Rules Induction for the to-use best algorithm because the accuracy is good and the model is very easy to interpret.

The Rules Induction with our whole data set results in the following rule model:

• if "link" ≤ 6.500 and "free" > 1.500 and "conclusion" > 7.500 then Computer Science (21 / 0)
• if "true" > 13.500 and "browser" ≤ 3.500 then Information Science (0 / 26)
• if "average" > 3.500 then Computer Science (9 / 0)
• if "employees" ≤ 5.500 then Information Science (0 / 8)
• if "procedure" ≤ 4 then Computer Science (8 / 0)
• else Information Science (0 / 2)

correct:

74 out of 74 training examples.