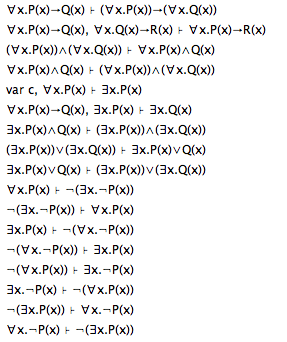Beweren en bewijzen/de zuilen/Zekerheid/5. Natuurlijke deductie

literatuur deductieschema Van Benthem Hoofdst. 4 t/m 4.2 Bestand:College-110601.pdf

Waarom nóg een bewijssysteem?

We introduceren nu het systeem van natuurlijke deductie terwijl het systeem van semantische tableaus al bekend is. Waarom?

Na een inleiding met voorbeelden voor correcte en foute redeneringen (hoofdstuk Overtuigen) hebben we de begrippen stelling en bewijs gedefinieerd en de betekenis van logische formules d.m.v. waarheidstabellen vastgelegd. Met waarheidstabellen kan men nagaan of een stelling klopt, maar dat is omslachtig. In plaats van een grote waarheidstabel kolom voor kolom in te vullen gaat men liever systematisch op zoek naar een tegenvoorbeeld, waarbij men met behulp van een slim gekozen formalisme, semantische tableaus, voorkomt dat men iets vergeet. Bij stellingen in propositielogica werkt dit heel goed. Als een stelling niet klopt, vindt men ten minste één situatie waarvoor ze niet geldt. Als een soort van bijproduct levert dat op dat als een tableau systematisch (en correct!) is uitgewerkt zonder tegenvoorbeelden op te leveren, er blijkbaar geen tegenvoorbeelden zijn en de stelling dus waar is. In zekere zin levert dit dus een indirect bewijs van de stelling op, maar geen inzicht in de stelling.

Daarmee hebben we ons verwijderd van het redeneren uit het inleidende hoofdstuk. Bovendien werken tableaus voor predicaatlogica lang niet zo goed.

Wie snel een tegenvoorbeeld in propositielogica wil vinden, kan het beste een tableau maken. Wie wil begrijpen waarom een stelling (in propositie- of predicaatlogica) werkelijk geldt, kan beter redeneren zoals in de inleiding geschetst en met een geschikt formalisme de stand van zaken bijhouden en voorkomen dat er fouten gemaakt of schakels in de redenering vergeten worden. Het formalisme dat we met dit doel introduceren heet natuurlijke deductie.

Het doel van natuurlijke deductie is het bewijzen van een stelling die geldig is. Als men probeert een niet kloppende stelling te bewijzen, is er geen duidelijk 'afbreek'-criterium in deze methode aanwezig. Vanwege de aanwezigheid van 'creatieve stappen' die op elk moment toegepast kunnen worden, is het altijd de vraag of een 'bewijs' niet afgemaakt kan worden omdat men te weinig creativiteit bezit om de techniek te gebruiken of omdat de stelling simpelweg niet deugt. Daarom is het systeem van de natuurlijke deductie ongeschikt om systematisch tegenvoorbeelden te vinden. Daar staat tegenover dat men met wat ervaring bij het maken van bewijzen met natuurlijke deductie merkt welke (ware) aannames men bij het modelleren van een correctheidsvraagstuk vergeten is.

Bij het modelleren van systemen vergeet men namelijk regelmatig dingen op te schrijven die vanzelfsprekend lijken. Men schrijft bijvoorbeeld in de specificatie van een reactorvat op dat het leegloopt als de kraan open staat, maar vergeet te vermelden dat het zijn inhoud bewaart zolang de kraan dicht is. Als men dan iets wil bewijzen over een raffinaderij waarvan dat vat een onderdeel is, zal het bewijs niet lukken. Maar men komt wel tot inzicht wat men bij het modelleren van dat onderdeel vergeten is.

Formeel ondersteund redeneren

Dus terug naar het redeneren uit het inleidend hoofdstuk Overtuigen!

Daar vinden we de volgende aannames (genummerd) en conclusies (onderscheiden door kleine letters). Ze leven links boven in de vier werelden. We geven ze hieronder ook weer als formules (rechts boven in de vier werelden). Het bijbehorende domeinmodel moge de lezer zelf bedenken.

Nr.	Natuurlijke taal	Formele taal
aannames
(1)	Jan vertelt een verhaal en Piet leest de krant.	JV ∧ PK
(2)	Als Jan een verhaal vertelt, dan lacht Marie.	JV → ML
(3)	Als Piet de krant leest, dan kijkt Wilma tv.	PK → WT
(4)	Kees is thuis of niet.	KT ∨ ¬KT
(5)	Als Wilma tv kijkt, is Kees niet thuis.	WT → ¬ KT
(6)	Als Kees thuis is en Marie lacht dan is hij gelukkig.	KT ∧ ML → KG
(7)	Als Kees niet thuis is, is hij gelukkig.	¬ KT → KG
conclusies
(a)	Jan vertelt een verhaal en Piet leest de krant.	JV ∧ PK
(b)	Jan vertelt een verhaal.	JV
(c)	Piet leest de krant.	PK
(d)	Marie lacht.	ML
(e)	Wilma kijkt tv.	WT
(f)	Wilma kijkt tv en Marie lacht.	ML ∧ WT
(g)	Als Wilma tv kijkt, is Kees gelukkig.	WT → KG
(h)	Marie lacht of Piet leest de krant.	ML ∨ PK
(i)	Kees is gelukkig.	KG

In Overtuigen vinden we ook bewijzen in natuurlijke taal voor alle conclusies. Zulke bewijzen hadden de Oude Grieken, bijvoorbeeld Euklides en Archimedes ook al prima kunnen geven. Maar wij kunnen nu meer. Ons begrip van het redeneren verhoudt zich tot dat van de Oude Grieken als het begrip van de Oude Grieken van het rekenen tot dat van de Babyloniërs.

De Babyloniërs konden al prima rekenen. Dat komt omdat hun belastingdienst de opbrengst van akkers in verhouding tot hun oppervlak moest kunnen bepalen. Voor een ingewikkeld veld konden ze precies de grootte uitrekenen en vermenigvuldigen met de waarde van de gemiddelde opbrengst. Het werkte. De staat was tevreden. Maar niemand vroeg zich af wat dat rekenen en de wetten waaraan het onderworpen was eigenlijk is.

De Grieken vroegen zich dat wel af. Ze wilden begrijpen waarom twee vreemd gevormde akkers hetzelfde oppervlak (en dus dezelfde opbrengst) kunnen hebben en hoe men iemand anders van dit inzicht kan overtuigen. Ze ontwikkelden een cultuur van wiskundig bewijzen en konden voor ingewikkelde stellingen uit de meet- en rekenkunde systematisch en overtuigend beredeneren of deze geldig waren.

Maar ze vroegen zich nauwelijks af, wat waarheid en redeneren eigenlijk is. Ze pasten logica toe zo als de Babyloniers rekenen toepasten.

Pas in de 19e en 20e eeuw van onze tijdrekening lukte het om het redeneren – de logica – net zo goed en volledig te begrijpen als de Grieken de meetkunde en rekenkunde begrepen. Eén van de resultaten is het systeem van de natuurlijke deductie, dat het toestaat om alle mogelijke redeneringen uit een klein aantal exacte redeneerstappen op te bouwen, zoals bij het schaken alle mogelijke veldslagen uit alleen maar bewegingen volgens een klein aantal bewegingsregels bestaan. Sindsdien is exact, volledig, overtuigend redeneren net schaken: het kan erg zijn om het doel te bereiken, maar een kind [1] – of een computer! – kan controleren of men geen fouten maakt.

Deze regels zijn zelf ook weer met een formalisme beschreven. Daarbij staan de Griekse hoofletters Σ en Φ voor willekeurige verzamelingen van aannames en de kleine letters φ, ψ, α enz. voor beweringen. Binnen één redeneerstap betekenen gelijke Griekse letters precies hetzelfde, net als in algebraïsche formules als (a+b)²=a²+2 a b+b². Het teken ⊢ geeft aan: „Ik heb conform deze regels bewezen of ben aan het bewijzen dat dit een geldig gevolg is.” De regels zijn zo bedacht dat als je klaar bent met het bewijs voor Σ ⊢ φ zeker is dat Σ ⊨ φ. Wat je conform deze regels bewezen hebt is ook waar! Bij het schaken weet je alleen dat je dit abstracte spel gewonnen hebt. Over een echte veldslag weet je dan nog niets.

In het vervolg moet je het deductieschema|schema met deze regels steeds bij de hand hebben.

We leggen ze nu uit aan de hand van de aannames en conclusies uit de tabel hierboven.

Opmerking vooraf: binnen ons systeem van natuurlijke deductie is het verplicht om op elke regel precies te zeggen wat de aannames zijn. Op deze pagina willen we eigenlijk bovengenoemde beweringen bewijzen aan de hand van alle bovenstaande aannames. Echter, om ruimte en schrijfwerk te besparen, schrijven we hier bij de afleidingen alleen maar die aannames op die ook echt gebruikt worden.

Jan vertelt een verhaal en Piet leest de krant.

	hyp
JV ∧ PK ⊢ JV ∧ PK

De hyp-regel gebruik je om aan te geven dat niets meer te bewijzen is: de te bewijzen bewering is letterlijk een van de aannames. Interessant is deze regel niet, maar wel nodig om het eind van het spel te bepalen: Bij elke tak in de afleiding probeer je ervoor te zorgen dat rechts van de ⊢ er een formule staat die ook in het rijtje links van de formules staat. Dan ben je klaar.

Jan vertelt een verhaal.

hyp JV ∧ PK ⊢ JV ∧ PK	∧1E
JV ∧ PK ⊢ JV

Uit aanname (1) volgt dat Jan een verhaal vertelt en dat Piet de krant leest. Dit is hier aangegeven d.m.v. de hyp-regel. Dus in het bijzonder geldt dat Jan een verhaal vertelt. We zien hier hoe de ∧1E-regel de ∧ elimineert en alleen de eerste helft van die formule behoudt, tenminste als je deze stap van boven naar beneden leest.

Als je een bewijs aan het zoeken bent kun je beter systematisch van beneden naar boven werken: je begint onderaan een leeg vel met de te bewijzen stelling, in dit geval dat Jan een verhaal vertelt onder bepaalde aannames. Dan kies je uit alle deductieregels een die je dichter bij de aannames brengt. In dit geval is de ∧1E-regel een goede keus: om te bewijzen dat Jan een verhaal vertelt kun je beter bewijzen dat Jan een verhaal vertelt en nog iets anders geldt, in dit geval dat Piet de krant leest. Want dat staat al in onze aannames: hyp.

Piet leest de krant.

hyp JV ∧ PK ⊢ JV ∧ PK	∧2E
JV ∧ PK ⊢ PK

En hier wordt natuurlijk juist de tweede helft behouden bij de ∧2E-regel.

Marie lacht.

hyp JV ∧ PK, JV → ML ⊢ JV ∧ PK ∧1E JV ∧ PK, JV → ML ⊢ JV	hyp JV ∧ PK, JV → ML ⊢ JV → ML	→E
JV ∧ PK, JV → ML ⊢ ML

Hopelijk herken je hier het verband met de natuurlijke taal: Uit aanname (2) volgt dat als Jan een verhaal vertelt, dan lacht Marie. Maar conclusie (b) toont aan dat Jan inderdaad een verhaal vertelt. En dus volgt uit (b) en (2) samen dat Marie lacht.

Er wordt eerst een bewijs geleverd van JV en een (triviaal) bewijs van JV → ML. Vervolgens wordt de →E-regel dan gebruikt om te concluderen dat er ook een bewijs voor ML is gevonden.

Ook dit bewijs kun je het beste vinden door van beneden naar boven te werken. Je schrijft onderaan op wat je wilt bewijzen: dat onder allerlei aannames Marie lacht. Je bekijkt je aannames, en je ziet dat wat je wilt bewijzen volgt uit iets anders, in dit geval dat Jan een verhaal vertelt. Om te bewijzen dat Marie lacht moet je dus twee dingen bewijzen: dat iets het geval is en dat daaruit volgt wat je eigenlijk wilt bewijzen.

Wilma kijkt tv.

hyp JV ∧ PK, PK → WT ⊢ JV ∧ PK ∧2E JV ∧ PK, PK → WT ⊢ PK	hyp JV ∧ PK, PK → WT ⊢ PK → WT	→E
JV ∧ PK, PK → WT ⊢ WT

Wilma kijkt tv en Marie lacht.

hyp JV ∧ PK, JV → ML, PK → WT⊢ JV ∧ PK ∧2E JV ∧ PK, JV → ML, PK → WT ⊢ PK   hyp JV ∧ PK, JV → ML, PK → WT ⊢ PK → WT →E JV ∧ PK, JV → ML, PK → WT ⊢ WT	hyp JV ∧ PK, JV → ML, PK → WT ⊢ JV ∧ PK ∧1E JV ∧ PK, JV → ML, PK → WT ⊢ JV   hyp JV ∧ PK, JV → ML, PK → WT ⊢ JV → ML →E JV ∧ PK, JV → ML, PK → WT ⊢ ML	∧I
JV ∧ PK, JV → ML, PK → WT ⊢ WT ∧ ML

Aan de linkerkant wordt er eerst een bewijs gegeven van WT, aan de rechterkant van ML, en de ∧I-regel koppelt die bewijzen dan aan elkaar.

Als Wilma tv kijkt, is Kees gelukkig.

hyp WT → ¬ KT, ¬ KT → KG, WT ⊢ WT   hyp WT → ¬ KT, ¬ KT → KG, WT ⊢ WT → ¬ KT →E WT → ¬ KT, ¬ KT → KG, WT ⊢ ¬ KT   hyp WT → ¬ KT, ¬ KT → KG, WT ⊢ ¬ KT → KG →E WT → ¬ KT, ¬ KT → KG, WT ⊢ KG	→I
WT → ¬ KT, ¬ KT → KG ⊢ WT → KG

De →I-regel komt dus overeen met de opmerking bij het bewijs in natuurlijke taal dat we de WT als extra aanname mogen gebruiken.

Marie lacht of Piet leest de krant.

Bij de natuurlijke taal hebben we al gezien dat we de laatste stap konden zetten uitgaande van conclusie (d) Marie lacht of juist van (c) Piet leest de krant. Hier eerst het bewijs dat gebruik maakt van het feit dat Marie lacht.

hyp JV ∧ PK, JV → ML ⊢ JV ∧ PK ∧1E JV ∧ PK, JV → ML ⊢ JV   hyp JV ∧ PK, JV → ML ⊢ JV → ML →E JV ∧ PK, JV → ML ⊢ ML	∨1I
JV ∧ PK, JV → ML ⊢ ML ∨ PK

Nu het bewijs uitgaande van het feit dat Piet de krant leest.

hyp JV ∧ PK ⊢ JV ∧ PK ∧2E JV ∧ PK ⊢ PK	∨2I
JV ∧ PK ⊢ ML ∨ PK

We zien dat deze boom korter is. Dat komt natuurlijk direct doordat de bewering Piet leest de krant in minder stappen te bewijzen is dan de bewering Marie lacht. Ook al weet je misschien van beide delen dat ze waar zijn, de keuze voor een van de twee kan wezenlijk meer of minder werk opleveren bij het afwerken van het bewijs.

Kees is gelukkig.

Eerst het bewijs waarbij geen gebruik wordt gemaakt van de ∨E-regel.

hyp JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ JV ∧ PK ∧2E JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ PK   hyp JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ PK → WT →E JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ WT   hyp JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ WT → ¬ KT →E JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ ¬ KT	hyp JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ ¬ KT → KG	→E
JV ∧ PK, PK → WT, WT → ¬ KT, ¬ KT → KG ⊢ KG

Nu de variant waarbij gebruik wordt gemaakt van de ∨E-regel.

hyp JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG ⊢ KT ∨ ¬ KT	hyp JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ KT   hyp JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ JV ∧ PK ∧1E JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ JV   hyp JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ JV → ML →E JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ ML ∧I JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ KT ∧ ML   hyp JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ KT ∧ ML → KG →E JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, KT ⊢ KG	hyp JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, ¬KT ⊢ ¬ KT   hyp JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, ¬KT ⊢ ¬ KT → KG →E JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG, ¬KT ⊢ KG	∨E
JV ∧ PK, JV → ML, KT ∨¬ KT, KT ∧ ML → KG, ¬ KT → KG ⊢ KG

Bij dit voorbeeld is het dus niet noodzakelijk om de aanname KT ∨ ¬ KT te gebruiken met de ∨E-regel, maar in de praktijk is het vaak handig om deze regel toe te passen op een formule van de vorm P ∨ ¬ P. In dit voorbeeld was de formule KT ∨ ¬ KT expliciet opgenomen bij de aannames, maar in zijn algemeenheid hoeft dat niet. Het is niet makkelijk, maar je kunt binnen ons systeem van regels altijd een afleidingsboom maken met ⊢ P ∨ ¬ P als conclusie, voor willekeurige formules P. Zie hier.

Het regelsysteem van de natuurlijke deductie

We hebben hierboven gezien hoe bewijzen in natuurlijke taal systematisch genoteerd kunnen worden en welke patronen daarbij optreden. We vatten samen.

Een correcte redenering loopt volgens bepaalde redeneerregels. Deze regels zijn zo gemaakt dat ze bij de fysieke realiteit passen. Zie De vier werelden in 3. Formalisering:

1. Als de realiteit de beweringen b1, b2, ..., bn waar maakt,
2. en als B uit b1, b2, ..., bn volgens de redeneerregels afgeleid kan worden
3. dan maakt de realiteit ook B waar.

Het systeem van de natuurlijke deductie bestaat uit 16 zulke redeneerregels (maar 12 als je je beperkt tot de propositielogica): deductieschema. Ze zijn streng formeel en passen bij de logische voegtekens ∧, ∨ ¬, → en de kwantoren ∀ en ∃.

Verschil tussen ⊢ en ⊨

De zogenaamde Turnstile, ⊢, wordt gebruikt als het gaat om syntactische afleidbaarheid. Puur aan de hand van syntactische manipulaties kan men proberen afleidingsbomen met een bepaalde conclusie op te stellen. Σ ⊢ φ betekent dat φ afleidbaar is uit een rij formules Σ. (Op het college van 18 mei 2011 is gezegd dat je dit ook mag uitspreken als Σ bewijst φ.)

⊢ φ betekent dus dat φ zonder enige aanname afleidbaar is. Soms zegt men dan dat φ een stelling is. Soms laat men dan de ⊢ zelfs weg.

De zogenaamde Double Turnstile, ⊨, (die we al kennen) wordt gebruikt als het gaat om semantische geldigheid. Hierbij gaat het er om of een bepaalde bewering semantisch waar is. Σ ⊨ φ betekent dat φ een logisch gevolg is van een rij formules Σ.

⊨ φ betekent dus dat φ (zonder enige aanname) een tautologie is.

In mooie systemen als propositielogica en (eenvoudige) predikaatlogica geldt er een equivalentie tussen beide begrippen: Σ ⊢ φ ⇔ Σ ⊨ φ. Wat je met regeltjes kunt bewijzen is ook werkelijk waar, en alles wat waar is kun je ook bewijzen.

Bedenken en presenteren van redeneringen

Redeneringen kunnen op twee manieren gepresenteerd worden:

1. stapsgewijs naar de conclusie toe werkend: „Het regent. Als het regent is de grond nat. Dus is de grond nat. Het vriest. Als de grond nat is en het vriest, is er glad ijs. Dus is er glad ijs.”
2. stapsgewijs vanuit de te bewijzen conclusie terugwerkend: „Er is gladheid. Want als de grond nat is en het vriest, ís er gladheid. En het vriest. En de grond is nat als het regent, hetgeen het nu doet.”

In welke volgorde een redenering gepresenteerd wordt, maakt voor de correctheid van de redenering niet uit. Essentieel is dat alle stukjes van de redenering naadloos op elkaar aansluiten. Een bewijssysteem helpt je bij het controleren.

Als je een bewijs opstelt conform deze regels, is het eindresultaat een „bewijsboom” die de lezer op beide manieren kan lezen: stapsgewijs van de aannames naar de conclusie of van de conclusie naar de aannames.

De regels worden onderverdeeld in introductieregels en eliminatieregels. Deze termen kunnen misleidend zijn! „Introductie” betekent: Als je van boven de streep van een bewijsregel naar beneden redeneert, wordt het bewuste voegteken geïntroduceerd. Als je van beneden de streep naar boven redeneert, gebruik je zo'n introductieregel echter om het voegteken juist weg te werken.

Conjunctie en disjunctie

	introductie	eliminatie
∧	∧I: beide nodige bewijzen	∧E: kennis toespitsen op één van twee zekere gevallen
	... ⊢ 0+0=0*0 ... ⊢ 2+2=2*2 ... ⊢ 0+0=0*0 ∧ 2+2=2*2	... ⊢ isKoning x ∧ leeft x ... ⊢ leeft x
∨	∨I: kennis vervagen tot twee mogelijke gevallen	∨E: onderscheiding van beide mogelijke gevallen
	... ⊢ 2*2=2^2 ... ⊢ 0*0=0^0 ∨ 2*2=2^2	... ⊢ isRijk x ∨ isGelukkig x ..., isRijk x ⊢ isTevreden x ..., isGelukkig x ⊢ isTevreden x ... ⊢ isTevreden x

Quantoren

De regels voor ∀ en ∃ kun je het best begrijpen en onthouden als je ze opvat als „oneindige” varianten van de regels voor ∧ en ∨. Omdat we niet oneindig veel gevallen kunnen opschrijven in een gevalsonderscheiding en evenmin oneindig veel bewijzen, moeten we iets algemeens opschrijven. Daarbij is iets aan de hand met variabelen en termen. Bij elke regel staan „kleine lettertjes” die aangeven wat men wel en niet mag invullen. Soms gaat het om een concreet speciaal geval, soms juist om een „onbesproken variabele”. Het is absoluut belangrijk dat je deze regels met behartiging van de kleine lettertjes toepast. Hier maakt men erg makkelijk zware fouten. Een computerprogramma als Jape of Coq tikt je op de vingers bij zulke fouten.

Het samenspel tussen

• conjunctie en disjunctie
• universeel en existentieel
• introductie en eliminatie
• onbesproken en specifiek
• boven en beneden
• links en rechts
• mogelijk en nodig

is van grote symmetrische schoonheid. Als je dat een keer begrijpt, vergeet je het nooit meer.

	introductie	eliminatie
∀	∀I: een bewijs voor een willekeurig geval staat gelijk aan alle nodige bewijzen	∀E: universele kennis toespitsen
	Onbesproken variabele in de te bewijzen bewering (rechts) Wat we voor een onbesproken variabele bewijzen, is voor alles bewezen – maar die variabele mag dan ook echt helemaal geen specifieke kennis transporteren, vandaar „onbesproken”. Deductieschema: y komt niet als vrije variabele voor in Σ noch in ∀x,α	Speciaal geval onder de streep Wat universeel geldt, geldt ook voor een specifiek geval, dus voor elke term. Deductieschema: term t is een zeker speciaal geval
	... ⊢ even n → oneven n+1 ... ⊢ ∀x:N, exen x → oneven (x+1) „Ik heb het bewezen voor 2, 4 en 6. Maar op die manier moet ik oneindig lang doorgaan.” „Kijk, ik kan het bewijzen voor n.” „Wat is n dan?” „Een onbesproken variabele, dat betekent dat je er elk willekeurig getal voor mag invullen.” „En dan?” „Dan krijg je voor dat getal een concreet bewijs.” „Dan geloof ik het wel.”	... ⊢ ∀x:R, x*x≥0 ... ⊢ 3*3≥0 „We weten dat het geldt voor alle elementen van R.” „3 is een specifiek geval van R.” „Dus in het bijzonder geldt 3*3≥0.” Merk op dat de term (3-(2*4)) ook een specifiek geval van R is. Met hetzelfde gemak had dus ook de conclusie kunnen worden getrokken dat (3-(2*4))*(3-(2*4))≥0.
∃	∃I: specifieke kennis vervagen	∃E: aanname van een willekeurig geval staat gelijk aan onderscheiding van alle mogelijke gevallen
	Speciaal geval boven de streep Wat voor een specifiek geval geldt, geldt minstens voor één geval. Deductieschema: term t is een zeker speciaal geval	Onbesproken variabele in een extra aanname (links van de ⊢) Omgaan met onvolledige kennis: „Geef het beestje een naam” – maar dan zonder specifieke kennis erin te smokkelen, vandaar „onbesproken”. Deductieschema: y komt niet als vrije variabele voor in γ noch in Σ noch in ∃x,α
	... ⊢ 3*3>0 ... ⊢ ∃x:R, x*x>0 „3 is een specifiek geval van R.” „Voor 3 weten we dat 3*3>0.” „Dus we weten zeker dat er een element van R is waarvoor het geldt.”	... ⊢ ∃n:N, n+n=n*n ..., y+y=y*y ⊢ ¬(∀x:N, x*x>x+x) ... ⊢ ¬(∀x:N, x*x>x+x) „Ik herinner me dat er een getal is waarvan het dubbele gelijk is aan zijn tweede macht. Dat moet een tegenspraak opleveren!” „Ok, stel dat dit getal 3 is.” „Nee, dat mag niet, want we kennen het niet. Maar laten we dit onbekende getal y noemen! Dan hoeven we niet altijd te zeggen: ,het getal, waarvan we weten dat het bestaat en waarvan het dubbele gelijk is aan zijn tweede macht’.” „Schept dat geen verwarring dan?” „Nee, want over y hebben we het nog nooit gehad. Dat is niet per ongeluk gelijk aan iets anders.”

De overige kleine lettertjes zijn de volgende:

• ∀_I: y komt uitsluitend als vrije variabele voor in α[x:=y]
• ∀_E: vrije variabelen in t moeten ook vrij zijn in α[x:=t]
• ∃_I: vrije variabelen in t moeten ook vrij zijn in α[x:=t]
• ∃_E: y komt uitsluitend als vrije variabele voor in α[x:=y]

Deze kleine lettertjes zijn allen bedoeld om rare substituties tegen te gaan. Een voorbeeld van zo'n verkeerde substitutie is: in (∀ x:N, ∀ y:N, R x y) kies ik het speciale geval x:=3*y en krijg ik (∀ y:N, R (3*y) y). Immers, men mag voor x wel van alles invullen maar dat moet niet opeens gebonden raken. In het voorbeeld raakt y in 3*y gebonden.

Wat is een „vrije” en wat een „onbesproken” variabele?

Eigenlijk zouden we, om „vrije” variabelen te definiëren, exacter moeten spreken over een vrij voorkomen van een variabele. Dezelfde variabele(naam) kan in één formule namelijk vrij én gebonden optreden (dat raad ik af, maar het is niet verboden). Als een variabele x in het bereik van een kwantor ∀x of ∃x voorkomt, dan is ze gebonden, anders is ze vrij. Voorbeeld: In de formule ∀x:T, x=y ∨ (∃y:T, z<y) komt x twee keer gebonden voor; het eerste voorkomen van y is vrij en de twee volgende zijn ook gebonden; z komt één keer vrij voor.

Maar wat als een variabele y helemaal niet in de formule voorkomt? Dan kunnen we zeggen dat y onbesproken is (tenminste voorzover het die formule betreft). Meestal gaat het erom dat een variabele onbesproken is met betrekking tot een aantal formules; daarmee bedoelen we dan dat de variabele in geen enkele van die formules mag voorkomen. (Strict gesproken mag een variabele soms wel gebonden voorkomen, maar dat is weer een situatie die je het beste vermijdt.)

Bewijzen met de speciale regels om met getallen te kunnen werken

In het hier gebruikte bewijssysteem kun je een tak alleen maar afsluiten met de hyp-regel of met de LEM-regel. Er zijn echter stellingen te bedenken die je zou willen bewijzen, maar waarbij dat niet lukt omdat je bij je doel niet precies een van de aannames kunt krijgen. Neem bijvoorbeeld deze stelling waarbij R staat voor de reële getallen:

∀ x:R, x > 1 → P x ⊢ ∀ x:R, x ≥ 5 → P x

Als het gegeven is dat voor alle x>1 geldt dat P x waar is, dan is het ook zeker waar dat P x geldt voor alle x≥5, want er is geen enkele x≥5 waarvoor niet geldt x>1. Hoe kunnen we dit nu bewijzen met natuurlijke deductie?

hyp ∀ x:R, x > 1 → P x, z ≥ 5 ⊢ ∀ x:R, x> 1 → P x ∀E ∀ x:R, x > 1 → P x, z ≥ 5 ⊢ z > 1 → P z   lins ∀ x:R, x > 1 → P x, z ≥ 5 ⊢ z > 1 →E ∀ x:R, x > 1 → P x, z ≥ 5 ⊢ P z →I ∀ x:R, x > 1 → P x ⊢ z ≥ 5 → P z	∀I
∀ x:R, x > 1 → P x ⊢ ∀ x:R, x ≥ 5 → P x

Je ziet dat er een truc is gebruikt om de zwakkere conclusie z>1 uit de sterkere z≥5 af te leiden. We maken hier gebruik van algemene wiskundige kennis over de reële getallen. En vervolgens kan het bewijs weer gewoon met een hyp-regel worden afgesloten.

Concreet hebben we hier dus de nieuwe lins-regel toegevoegd:

	lins
Σ ⊢ α

die mogen worden toegepast als α een simpele (niet-samengestelde) formule is waarvoor ook nog geldt: Σ impliceert α op basis van de eigenschappen van de reële getallen.

Een ander voorbeeld waarbij we een extre regel nodig kunnen hebben is om ervoor te zorgen dat ingewikkelde termen precies overeenkomen bij bijvoorbeeld een ∀E. Bekijk het volgende voorbeeld:

hyp ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42) ⊢ ∃ t:T, P (t–42)	hyp ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42), P (y–42) ⊢ ∀ t:T, P t → Q (37+t) ∀E ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42), P (y–42) ⊢ P (y–42) → Q (37 + (y–42))   lins ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42), P (y–42) ⊢ (y–5) = ((37+ (y–42)) subs ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42), P (y–42) ⊢ P (y–42) → Q (y–5)   hyp ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42), P (y–42) ⊢ P (y–42) →E ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42), P (y–42) ⊢ Q (y–5) ∃I ∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42), P (y–42) ⊢ ∃ t:T, Q t	∃E
∀ t:T, P t → Q (37+t), ∃ t:T, P (t–42) ⊢ ∃ t:T, Q t

Bij de toepassing van ∀E hebben we te maken met een α, een x en een t volgens de instantiatieregel. Hier geldt α = P t → Q (37+t), x = t en t = (y–42). Onder de streep moet dan precies α[x:=t] komen te staan, oftewel P (y–42) → Q (37+(y–42)). Maar zonder die subs-regel zou er P (y–42) → Q (y–5) hebben gestaan en dat is dus niet exact gelijk aan α[x:=t]. Vandaar dat die subs-regel om (y–5) te herschrijven naar het equivalente (37+(y–42)) noodzakelijk is. Overigens had men deze subs-regel wel kunnen voorkomen door bij de ∃I niet (y–5) maar meteen (37+(y–42)) als term in te vullen.

Uiteraard mag men niet zomaar substituties toepassen. Hier hebben we de term (y– 5) vervangen door (27+(y– 42)). Maar dan moeten we natuurlijk wel bewijzen dat dis substitutie te rechtvaardigen is. Vandaar de tweede bewijsverplichting. Vaak zal het overigens zo zijn dat de bewijsverplichting op de gelijkheid met de lins-regel kan worden afgesloten.

Samengevat levert dit dus de volgende subs-regel op:

Σ ⊢ α[t1:=t2]	Σ ⊢ t1 = t2	subs
Σ ⊢ α

Voor het werken met intervallen is er een speciale variant van de subs-regel. In onze taal mogen we iets schrijven als 't ∈ [a,b]'. Echter als we stellingen willen bewijzen lopen we vaak tegen het feit aan dat de gegevens in de aannames wel voldoende zijn om de stelling te bewijzen, maar niet precies passen bij het gegeven interval. Bijvoorbeeld omdat we in de aannames weten dat iets voor alle t ∈ [3,14] geldt, terwijl we moeten bewijzen dat het geldt voor t ∈ (6,10]. Uiteraard moet dit kunnen, want de conclusie is duidelijk zwakker dan de aanname. Om dit aan te kunnen moeten we de intervalnotatie omschrijven naar een conjunctie. Dat kan want t ∈ (6,10] betekent natuurlijk precies hetzelfde als 6 < t ∧ t ≤ 10. Vervolgens gebruiken we dan weer de regels als ∧I, →E en →I om de stelling zo op te schrijven dat we nog maar een simpele (enkelvoudige) conclusie hebben die elementair uit de aannames volgt en die we dus met de lins-regel kunnen afleiden.

Hiervoor gebruiken we de zogenaamde int-regel:

Σ ⊢ α[t ∈ [a,b] := a ≤ t ∧ t ≤ b]	int
Σ ⊢ α

In dit sjabloon is uitgegaan van een interval dat aan beide kanten gesloten is. Uiteraard werkt de regel ook voor open of halfopen intervallen, maar op de plaats waar een interval halfopen is moet natuurlijk een < gebruikt worden in plaats van de < in de regel hierboven. Zie deze pagina voor voorbeelden waar daadwerkelijk gerekend moet worden met deze lins-, subs- en int-regel.

Tenslotte vermelden we hier nog een regel die enkel en alleen tot doel heeft om een bepaalde notatie in onze grammatica om te schrijven naar een andere notatie waardoor de kennis over de bijbehorende getallen expliciet als vergelijking zichtbaar gemaakt kan worden. We mogen namelijk schrijven '∀ t:[a,b], P t'. Echter, in systemen waar dit soort intervallen niet zo mogen worden genoteerd (zoals in Coq) moeten we zo'n formule kunnen herschrijven tot '∀ t:T, t ∈ [a,b] → P t'. En net zo kunnen we '∃ t:[a,b], P t' herschrijven tot '∃ t:T, t ∈ [a,b] ∧ P t'. Hierbij moet T natuurlijk wel een type zijn waarbij het zin heeft om van een interval te spreken. Vaak zal T overeenkomen met de reële getallen.

Hiervoor gebruiken we de volgende regels:

Σ ⊢ ∀ t:T, t ∈ [a,b] → α	∀dom
Σ ⊢ ∀ t:[a,b], α

en

Σ ⊢ ∃ t:T, t ∈ [a,b] ∧ α	∃dom
Σ ⊢ ∃ t:[a,b], α

Uiteraard kan de regel ook worden gebruikt voor de andere intervallen [a,b), (a,b] en (a,b). Merk op dat hier weer de gebruikelijke combinatie van ∀+→ en ∃+∧ te zien is.

De manier van opschrijven van formele bewijzen

Hier gaat het even niet om de vraag hoe je op een bewijs komt, maar alleen erom, hoe je een eenmaal gevonden bewijs presenteert. Formele bewijzen met natuurlijke deductie – ook afleidingen genoemd – kun je op allerlei manieren opschrijven. In deze cursus zie je er drie langskomen:

„kale” bomen

Veel logici, zo ook Van Benthem, schrijven hun bewijzen het liefst op deze manier op. Je moet deze bomen kunnen lezen alleen al om het boek te kunnen begrijpen. Hier (met dank aan Marc Schoolderman) de kale boom van een bewijs voor P of niet P:

1 p p ∨ ¬p 2 ¬(p ∨ ¬p) [–1] ¬p p ∨ ¬p	3 ¬(p ∨ ¬p)	[–2,–3]
p ∨ ¬p

Deze notatie geeft de essentie weer, en de structuur van de redenering is duidelijk te zien voor mensen die goed geoefend zijn in het lezen van dit soort bomen. Anderen vinden deze bomen moeilijk te lezen. Het begint ermee dat men moet achterhalen, welke stelling hier eigenlijk bewezen wordt. De conclusie staat natuurlijk onderaan, men bewijst dus:

... ⊢ p ∨ ¬p

Links van de ⊢ moeten alle aannames komen die niet onderweg ingetrokken zijn. Bij grotere bomen moet men uiterst zorgvuldig kijken. In dit geval hier zijn alle aannames ingetrokken. Over blijft dus:

⊢ p ∨ ¬p

Als je zeker bent dat je goed weet wat je doet en als dat ook klopt, is dit een economische manier van opschrijven, zeker in klad, tijdens het bedenken van een bewijs. De ervaring in zoveel jaar Beweren en bewijzen leert echter dat deze manier tot misverstanden en fouten kan leiden zolang je niet 100% begrijpt wat je aan het doen bent. In het belang van je eigen veiligheid verlangen we daarom in het tentamen de volgende manier.

Bomen met sequenten

Achter voorbeeld 4.3 staat in Logica voor Informatica een boom met achter elke knoop de geldige aannames tussen accolades. Dat is een ongebruikelijke notatie. Veel bewijsassistenten en leerboeken schrijven hetzelfde net iets anders op, zodat overal de volledige, op dit moment geldige stelling staat:

¬(p ∨ ¬p), p ⊢ p [∨I] ¬(p ∨ ¬p), p ⊢ p ∨ ¬p ¬(p ∨ ¬p), p ⊢ ¬(p ∨ ¬ p) [¬I] ¬(p ∨ ¬p) ⊢ ¬p [∨I] ¬(p ∨ ¬p) ⊢ p ∨ ¬p	¬(p ∨ ¬ p) ⊢ ¬(p ∨ ¬p)	[¬E*]
⊢ p ∨ ¬p

Deze manier van opschrijven past precies bij het deductieschema. Dit is ook in principe de manier die we op het tentamen verlangen. Het voordeel is dat je op elke plek lokaal, d.w.z. zonder de hele boom door te pluizen, precies ziet wat hier bewezen wordt. Of een bewijsstap juist is, kun je met het deductieschema bij de hand controleren door precies te kijken wat boven en onder een streep staat.

Fitch-stijl

Er is een tussenvorm, die de voordelen van beide notaties verenigt en het extra voordeel heeft, dat ook grote bewijzen (wat de breedte betreft) op één pagina passen. Een voorbeeld:

1			¬(p ∨ ¬p)			hyp
2				p		hyp
3				p ∨ ¬p		∨I 2
5			¬p			¬I 2,3,1
6			p ∨ ¬p			∨I 5
7		p ∨ ¬p				¬E* 1,6

De bewijsboom die hiermee overeenkomt staat hier.

Om dit te lezen moet men weten dat op elke plek alle aannames gelden die erboven staan. Intrekkingen worden niet weergegeven door nummertjes maar door kaders. Daar staat tegenover dat de structuur van de vertakking weergegeven wordt door regelnummers. Als het kwartje valt, zie je hier dezelfde boom als het ware gekanteld en van boven. Het grootste voordeel is de compactheid.

De bewijzen in het tentamen zijn zo klein dat het vraagstuk „past het op één pagina” geen rol speelt. Daarom hoef je deze manier van opschrijven niet te beheersen. Je hoeft deze bewijzen ook niet te kunnen lezen. Maar voor het presenteren van een groot met de computer gemaakt bewijs in het werkstuk is dit de beste manier. Op eigen risico mag je deze methode ook gebruiken op het tentamen, maar dan met alle nummertjes!

De kunst van het bewijzen

Het vinden van een bewijs is in het algemeen niet berekenbaar. Het vereist creativiteit. Dat je bij het opstellen van een bewijs af en toe vastloopt is dus normaal. Je moet proberen, puzzelen, en als je de verkeerde afslag hebt genomen moet je de laatste stappen verwerpen en iets anders proberen.

Creatieve bewijsstappen

Bij een aantal bewijsstappen in het deductieschema staan boven de streep letters die onder de streep niet voorkomen. Hier mag je invullen wat je wilt – als het maar helpt. Dit zijn precies de bewijsstappen waar creativiteit nodig is. Hier mag je een geschikt tussenresultaat bedenken. („U mag zich nu uitkleden.”) Wat men bij weinig ervaring graag over het hoofd ziet: soms helpt het, twee gevallen te onderscheiden en voor elk geval een apart bewijs te maken. De regel voor gevalsonderscheiding (of-eliminatie) kun je toepassen als in je aannames een of voorkomt. Maar je kunt ze ook toepassen op een tautologie (die dan natuurlijk ook nog bewezen moet worden). Soms wil een gevalsonderscheiding over P ∨ ¬P eens helpen (die op zich niet eenvoudig te bewijzen is, zie P of niet P). Als je geen aanpak weet, bekijk je de te bewijzen stelling en vraag je je af of je het wel kunt onder de aanname dat een bepaalde propositie waar is, of juist onwaar.

Omgaan met onvolledige informatie – eliminatie versus introductie

Stel je wilt met natuurlijke deductie bewijzen: „op een dag sneeuwt het of staat er een regenboog”:

∃x, P x ∨ Q x

een logisch gevolg is van „op een dag sneeuwt het of op een, mogelijk andere, dag staat er een regenboog, al weet ik niet wat het wordt”:

(∃x, P x) ∨ (∃x, Q x)

Je begint dus met:

(∃x, P x) ∨ (∃x, Q x) ⊢ ∃x, P x ∨ Q x

Rechts staat een ∃. Wie niet goed nadenkt begint met ∃-introductie. Zeker: als bewijs dat er zo'n dag is voldoet één concreet voorbeeld. Maar kennen we op dit moment zo'n voorbeeld? Welke dag is dat dan, waarop het regent of sneeuwt? Wie de logica van de regels niet begrijpt en onverschillig wat aanmoddert probeert het met een variabele. Maar waar staat die voor?

(∃x, P x) ∨ (∃x, Q x) ⊢ P t ∨ Q t	∃I
(∃x, P x) ∨ (∃x, Q x) ⊢ ∃x, P x ∨ Q x

Met zulke onverschilligheid kun je door blijven modderen: Er staat een ∨ – dus zal het wel een ∨-introductie moeten wezen, al weet ik niet van welke kant. Het zal wel:

(∃x, P x) ∨ (∃x, Q x) ⊢ P t ∨1I (∃x, P x) ∨ (∃x, Q x) ⊢ P t ∨ Q t	∃I
(∃x, P x) ∨ (∃x, Q x) ⊢ ∃x, P x ∨ Q x

Wie echter nadenkt voelt op zijn logische klompen aan dat dit niets kan worden. Geen van de alternatieven is gegarandeerd op zichzelf waar. Bij onze aannames is sprake van onvolledige informatie: we weten dat er iets is, maar niet precies wat. Dit vraagt om gevalsonderscheidingen. De /bewijsstrategie zegt dan ook dat je eerst de ∨ aan de linker kant elimineert door twee gevallen te onderscheiden:

hyp (∃x, P x) ∨ (∃x, Q x) ⊢ (∃x, P x) ∨ (∃x, Q x)	Σ ;  ∃x, P x ⊢ ∃x, P x ∨ Q x	Σ ;  ∃x, Q x ⊢ ∃x, P x ∨ Q x	∨E
(∃x, P x) ∨ (∃x, Q x) ⊢ ∃x, P x ∨ Q x

De Σ staat hier als afkorting voor de oorspronkelijke aanname, die we overigens in deze twee takken niet meer nodig hebben. Met gezond verstand zien we dat we opgeschoten zijn. We concentreren ons nu op één van de twee open takken. De andere gaat op dezelfde manier. Te bewijzen:

Σ ;  ∃x, P x ⊢ ∃x, P x ∨ Q x

Nu kunnen we weer dezelfde domme fout maken en onverdroten ∃-introductie proberen. De /bewijsstrategie zegt daarentegen: We weten dat het op een dag sneeuwt, al weten we niet, op welke. Geef het beestje dan een naam. Laten we die onbekende dag, die er zeker is, y noemen.

hyp Σ ;  ∃x, P x ⊢ ∃x, P x	Σ ;  ∃x, P x ;  P y ⊢ ∃x, P x ∨ Q x	∃E
Σ ;  ∃x, P x ⊢ ∃x, P x ∨ Q x

En nu die geheimzinnige dag zijn naam heeft, loopt het als een trein. Op dag y sneeuwt het. Dan geldt ook dat het er sneeuwt of dat er een regenboog staat:

hyp Σ ;  ∃x, P x ;  P y ⊢ P y ∨1I Σ ;  ∃x, P x ;  P y ⊢ P y ∨ Q y	∃I
Σ ;  ∃x, P x ;  P y ⊢ ∃x, P x ∨ Q x

Standaardfouten

In Categorie:Bewijsfout staat een aantal veel gemaakte fouten. Sommige hebben te maken met het precieze toepassen van regels, in het bijzonder met de „kleine lettertjes” in de regels voor quantoren. Andere hebben te maken met een verleidelijke, maar verkeerde afslag. Zo is het vrijwel altijd verkeerd de ∨-eliminatie meteen toe te passen als de conclusie van de stelling een ∨ bevat. (Zie ook: P of niet P)

Strategie

Oefenstellingen propositielogica

Gedisciplineerd en systematisch werken helpt. En bij de keuze van bewijsregels helpt een strategie.

• Begin aan de onderkant van een leeg vel met de te bewijzen stelling, met alle aannames voor de ⊢.
• Schrijf in principe altijd bomen met sequenten op, zodat je op elke stap alle op dit moment geldige aannames ziet.
  • Als de Fitch-style beheerst, kun je die gebruiken.
  • Je mag tijdens de rit op eigen risico afkortingen gebruiken zolang je in klad werkt, maar bij de minste twijfel kun je beter nog eens alle geldige aannames uitschrijven.
• Vraag je bij elke stap twee dingen af:
  • Welke deductieregels komen hier in aanmerking? Heb ik er geen vergeten?
  • Leidt me wat nu boven de streep staat dichter bij het doel?
• Laat je leiden door de bewijsstrategie.
• Zodra boven een streep een creatieve keuze nodig is voor een letter, probeer eerst de eenvoudigste deelformules van mijn aannames en dan gecompliceerdere.

Reflectie

Stel, dat je vastloopt in een bewijs. Welke oorzaken kan dat hebben?

onbewijsbaar 

Misschien is wat je probeert te bewijzen helemaal geen stelling. Hetgeen tot de vraag leidt: hoe kan men dat weten? In het genoemde voorbeeld door een waarheidstabel te maken. Maar wat als dit niet te doen is?

fout bij de toepassing van een eerdere regel 

Er is een fout gemaakt in de natuurlijke deductie. Elke stap moet je dan nog eens nalopen en kijken of alle Griekse letters precies goed gesubstitueerd zijn. Voor hetzelfde geld heb je echter eerder een fout gemaakt waardoor je een bewijs rond krijgt voor iets dat helemaal geen stelling is. Je mag geen fouten maken, bij het bewijzen nog veel minder dan elders. Kijk elke stap meteen goed na. Controleer elke stap formeel, maar ook inhoudelijk! Gebruik een bewijsassistent die dat zorgvuldiger kan dan jij zelf!

eerder de verkeerde afslag genomen 

In veel situaties heb je de keus tussen een aantal verschillende regels. Zo kun je terecht komen in een doodlopende weg of een eindeloze lus.

Leren bewijzen

Oefenstellingen predicaatlogica

Bewijzen moet men oefenen! Ook mensen die op school nooit hoefden te werken omdat ze alle opdrachten zonder lang na te denken en zonder te proberen konden maken, zullen hier moeten oefenen. De kunst van het bewijzen is in dit opzicht vergelijkbaar met het bespelen van een muziekinstrument of het beoefenen van sport. Maar hoe kun je weten of je genoeg en op de juiste manier geoefend hebt?

1. Je moet de betekenis van de bewijsregels door en door begrijpen. Het gaat namelijk niet alleen om een formeel spelletje. Bij het schaken zijn de regels zo gegeven, ze hebben verder geen betekenis, je moet gewoon leren ze te beheersen. Bij het bewijzen zijn de regels van de natuurlijke deductie veel meer, namelijk een secure notatie voor redeneerstappen die de waarheid van beweringen overeind houden.   Quality Check   Ben je bij elke regel overtuigd dat deze een diepe waarheid uitdrukt en zo en niet anders moet zijn? Zo niet, moet je daar iets aan doen, bijvoorbeeld door met een medestudent of docent erover te praten of in deze werkplaats een vraag te stellen.
2. Je moet een blik krijgen voor fouten. Een voordeel bij natuurlijke deductie is dat men fouten lokaal kan opsporen, door telkens één stap te controleren, zonder de grote lijn te kennen. Daarom is Coq daar ook goed in.   Quality Check   Als je een handmatig bewijs door Coq laat controleren en Coq vindt een fout, zie je dan in dat en waarom het fout was? Kun je bij elke regel aangeven waarop men bij het controleren specifiek moet letten? D.w.z. wat de valkuilen zijn?
3. Je moet door oefenen de bewijsstrategie verinnerlijken zonder haar slaafs te volgen. Het is een strategie, maar soms kun je er beter van afwijken. Dit leer je alleen door te oefenen.   Quality Check   Hiernaast een rij oefenstellingen. Als je voor al deze stellingen ook zonder Coq een correct bewijs kunt produceren, kun je waarschijnlijk ook alle tentamens maken.

Grenzen: P of niet P ?

Beweren en bewijzen/de zuilen/Zekerheid/5. Natuurlijke deductie/P of niet P