Beweren en bewijzen/de opzet/gereedschap/Coq
Logisch redeneren is iets typisch menselijks. Of toch niet...
Er zijn zeer slimme computerprogramma's ontwikkeld die informatici en wiskundigen kunnen helpen bij het vinden en controleren van bewijzen voor beweringen of bij de controle op correctheid van algoritmes. Deze programma's heten bewijsassistenten. We zullen in dit college kennismaken met de Franse bewijsassistent Coq. Coq is beschikbaar via twee wegen:
- Op [1] kan men via Provers en dan Coq de Coq webinterface opstarten. Deze heeft als voordeel dat je het zo kunt gebruiken en bewijsbomen kunnen worden afgebeeld.
- Als installeerbaar programma, deze zal waarschijnlijk sneller werken, werkt off-line en bij een crash kun je zelf meteen opnieuw opstarten. De website geeft een goede installatiehandleiding. Je moet het bestand [2] downloaden en compileren om aan de slag te kunnen (nieuwste versies 15 april 2009). Dit bestand kan in de loop van de tijd veranderen. Neem daarom deze pagina op in je volglijst. Wij zijn benieuwd naar jullie ervaringen, maar kunnen geen technische ondersteuning geven. Het compileren kun je doen door het bestand in dezelfde directory te zetten als het bestand waarin je werkt, en dan op het knopje "Compile → Compile Buffer" klikt.
Hier zullen we beschrijven hoe de webinterface van Coq werkt.
Inhoud
- 1 Gebruik van de Coq webinterface
- 2 Invoer voor Coq
- 3 Coq voor domeinmodellen en beweringen in propositielogica
- 4 Coq voor domeinmodellen en beweringen in predikaatlogica
- 5 Een stelling opschrijven in Coq
- 6 Coq voor propositielogica
- 7 Coq voor predikaatlogica
- 8 Coq voor predikaatlogica met getallen, vergelijkingen en intervallen
- 9 Werken met eindige verzamelingen in Coq
- 10 Coq in Mac OS X
Gebruik van de Coq webinterface
In het linkervak kun je een opdracht voor Coq creëren en bewerken. Rechtsboven geeft Coq de uitvoer. Het vak rechtsonder wordt eventueel bij natuurlijke deductie gebruikt om de bewijsboom weer te geven. Boven het scherm zie je verschillende menu's. We zullen de belangrijkste hiervan behandelen.
Het File-menu heeft geen functie voor de anonieme login zoals beschreven in deze handleiding. Een gemaakt script kan het beste de bewaard worden door de tekst uit de webinterface naar een tekst bestand of een werkplaatspagina te kopiëren.
Het Display-menu stelt je in staat om een grafische weergave van het bewijs waar je mee bezig bent te verkrijgen in het schermvak rechtsonder. Standaard staat het ingesteld op No proofs. Met de optie Gentzen style tree proofs (statements) verschijnt een "kale" bewijsboom. Met Fitch style box proofs wordt het bewijs weergegeven in een stijl (genoemd naar de bedenker, zie Wikipedia over Frederic Brenton Fitch) die we in de cursus B&B niet behandelen. Met Gentzen style tree proofs (full sequents)' wordt de bewijsboom volledig weergegeven met alle aannames, met zogeheten sequenten. (Deze bewijsstijl is wederom vernoemd naar de bedenker ervan, zie Wikipedia over Gerhard Gentzen.)
Verder zie je nog een aantal pijltjes in de menubalk staan. Deze zijn voor het uitvoeren van commando's/regels. Diezelfde acties zijn ook via toetscombinaties uit te voeren.
| actie | symbool in menu | toetscombinatie |
|---|---|---|
| één commando uitvoeren | pijl omlaag | Ctrl-(pijl omlaag) |
| één commando ongedaan maken | pijl omhoog | Ctrl-(pijl omhoog) |
| tot de cursor uitvoeren | pijl met stip | Ctrl-Enter |
| de hele buffer uitvoeren | pijl omlaag met streep | Ctrl-(page down) |
| de hele buffer ongedaan maken | pijl omhoog met streep | Ctrl-(page up) |
De interface laat je zien welke regels er uitgevoerd zijn door die groen te kleuren. Die regels zijn dan niet meer te bewerken, tenzij je de uitvoering ervan weer ongedaan maakt, op bovengenoemde wijze.
Invoer voor Coq
De invoer voor Coq is dezelfde als voor onze taal, behalve dat symbolen in ASCII geschreven moeten worden.
- Op Beweren en bewijzen/de zuilen/Taal/2. Logica staat een tabel die de ASCII varianten van de operatoren toont.
- De eerste regel bevat
Require Import BenB.om de definities en bewijsregels voor deze cursus te laden. - In het onderstaande hoofstuk Coq voor domeinmodellen en beweringen wordt getoond hoe men een domeinmodel in Coq maakt.
-
Theoremgebruikt men om een theorema (ook wel stelling genoemd) aan te duiden en het bewijs ervan te starten. - De bewijsregels zijn te vinden op Beweren en bewijzen/de zuilen/Zekerheid/5. Natuurlijke deductie/deductieschema.
- Tijdens bewijzen kun je met
Focus 3direct naar het 3e subgoal gaan. Je zal nu de andere doelen niet zien, totdat je doel 3 bewezen hebt. Dan krijg je de andere doelen weer te zien. Wil je alle doelen weer te zien krijgen, gebruik danUnfocus.Pas op gebruik geenFocus 1het is niet erg nuttig, maar erger is dat Coq er heel erg langzaam van kan worden. - Een bewijs wordt afgesloten met
Qed. - Commentaar kan men plaatsen tussen (* en *).
Coq voor domeinmodellen en beweringen in propositielogica
In de propositielogica zien domeinmodellen er altijd heel eenvoudig uit. Dit komt omdat er maar één type is, namelijk Prop. In de file BenB die ingelezen dient te worden om over de specifieke regels voor deze cursus te beschikken, wordt als afkorting voor Prop de letter B gedefinieerd om aan te geven dat men over Booleans praat. Het is een kwestie van smaak welke men gebruikt, maar zorg er wel voor dat als je B als type-aanduiding gebruikt, je niet ook nog een variabele B aanmaakt.
Hier een voorbeeld van een universele radio (omdat hij in verschillende omstandigheden te gebruiken is doordat hij een interne AC/DC converter bevat).
| propositie | type | betekenis | meting | formele notatie zonder tabel |
|---|---|---|---|---|
| wissel110 | Prop | Er staat 110V op het externe aansluitpunt van de AC/DC converter. | Meten met een voltmeter | Variable wissel110: Prop. |
| wissel230 | Prop | Er staat 230V op het externe aansluitpunt van de AC/DC converter. | Meten met een voltmeter | Variable wissel230: Prop. |
| gelijk12 | Prop | Er staat 12V op het interne aansluitpunt van de AC/DC converter. | Meten met een voltmeter | Variable wissel110: Prop. |
| ontvangst | Prop | De antenne ontvangt radiosignalen. | ??? | Variable ontvangst: Prop. |
| muziek | Prop | De radio laat muziek horen. | Luisteren | Variable muziek: Prop. |
Een bewering die je hiermee kunt doen is bijvoorbeeld wissel110 /\ wissel230, die je dan met Check kunt controleren.
Check wissel110 /\ wissel230.
Omdat deze bewering helemaal klopt qua type, zal Coq als antwoord geven :B om aan te geven dat het een boolse bewering is. Let wel, Check zegt dus helemaal niets over het al dan niet waar zijn van zo'n bewering. Verder naar beneden op deze pagina wordt uitgelegd hoe je kunt bepalen of iets waar is of niet in de propositielogica.
Coq voor domeinmodellen en beweringen in predikaatlogica
Omdat de formele taal van de predikaatlogica die we gebruiken zeer nauw aansluit bij die van Coq, kunnen we Coq gebruiken om te controleren of het domeinmodel syntactisch correct is en of een bewering syntactisch correct is en past bij het domeinmodel. In het bijzonder krijgen we hier ingewikkeldere domeinmodellen omdat er nu wel verschillende types door elkaar kunnen worden gebruikt.
We herhalen een domeinmodel en bewering uit 3. Formalisering.
| type | betekenis (verzameling) | formele notatie zonder tabel | ||
|---|---|---|---|---|
| T | de tijd in reële getallen | Definition T := R. | ||
| K | de hoorbare klanken | Variable K: Set. | ||
| C | digitale beschrijving van klanken | Variable C: Set. | ||
| (t1...t2] | {t: T | t1< t ∧ t ≤ t2} | |||
| functie | type | betekenis | formele notatie zonder tabel | |
| duratie | (T→C)→T | duratie s: de duratie van een digitaal beschreven stuk s | Variable duratie: (T->C)->T. | |
| klank | C→K | klank c: de hoorbare klank bij de beschrijving c van een klank | Variable klank: C->K. | |
| predikaat | type | betekenis | meting | formele notatie zonder tabel |
| cd | T→(T→C)→B | cd t s: op moment t draait in de cd-speler een schijfje waarop stuk s staat | schijfje bekijken | Variable cd: T->(T->C)->B. |
| hoor | T→K→B | hoor t k: op moment t hoort men klank k | luisteren | Variable hoor: T->K->B. |
met bewering:
∀m: T, ∀s: T→C, (∀t: (0, duratie s], cd (m+t) s) -> (∀t: (0, duratie s], hoor (m+t) (klank (s t)))
We kunnen de consistentie in Coq controleren met de volgende invoer:
Require Import BenB. Definition T := R. Variable K: Set. Variable C: Set. Variable duratie: (T->C)->T. Variable klank: C->K. Variable cd: T->(T->C)->B. Variable hoor: T->K->B. Check forall m: T, forall s: T->C, (forall t: T, t in (0, duratie s] -> cd (m+t) s) -> (forall t: T, t in (0, duratie s] -> hoor (m+t) (klank (s t))).
De eerste regel importeert de juiste definities voor deze cursus. De volgende regels zijn precies zoals die in de laatste kolom van het domeinmodel. De laatste regel voert het commando Check uit om de bewering te controleren. Als de bewering 'klopt' geeft het commando het type van de bewering weer, in dit geval :B. De bewering is overigens iets anders opgeschreven dan hierboven, omdat Coq slechts in beperktere mate om kan gaan met intervallen.
De volgende tabel geeft aan hoe beweringen met universele en existentiële kwantoren over intervallen anders geschreven kunnen worden. Let op het verschil. Uiteraard kan voor (a, b] ook een ander interval zoals [a, b) worden ingevuld.
| bewering | alternatief | in Coq |
|---|---|---|
| ∀t: (a, b], P t | ∀t: T, t ∈ (a, b] → P t | forall t: T, t in (a, b] -> P t |
| ∃t: (a, b], P t | ∃t: T, t ∈ (a, b] ∧ P t | exists t: T, t in (a, b] /\ P t |
Als alles klopt zal Coq niet klagen.
Een stelling opschrijven in Coq
Stel we willen bewijzen m.b.v. Coq: P → Q, Q → R, P |- R. Er is geen manier om het |- teken en de kommas in Coq te schrijven. Coq kan in feite alleen bewijzen of een bewering een tautologie is. We hebben gezien dat men ook kan schrijven: (P → Q) ∧ (Q → R) ∧ P → R. Maar dit is erg onhandig omdat men 1 aanname krijgt in plaats van een verzameling van aannames. Om bijvoorbeeld R te concluderen uit de aanname moet men twee keer een con_e stap uitvoeren.
Handiger is het om alle komma's en de |- in implicaties te veranderen. Dit geeft een bewering die logisch equivalent is. Om precies te zijn moet je de volgende 5 stappen uitvoeren:
- plaats haakjes om iedere aanname en de conclusie
- schrijf nu implicaties voor iedere komma en voor het |- teken
- verwijder e.v.t. overbodige haakjes in de verkregen formule
- plaats de formule in Coq als 'Theorem' en begin het bewijs met 'Proof.'
- voer evenveel imp_i stappen uit als er komma's waren en een imp_i stap voor het |- teken
Stappen 1-4 zullen met voldoende ervaring in 1 keer gedaan kunnen worden.
Voor het bovenstaande voorbeeld zien de stappen 1-3 er als volgt uit:
- (P → Q), (Q → R), (P) |- (R)
- (P → Q) -> (Q → R) -> (P) -> (R)
- (P → Q) -> (Q → R) -> P -> R
Het begin van een Coq bewijs ziet er nu als volgt uit:
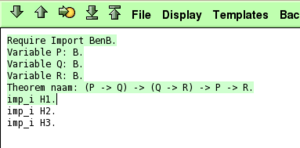
Require Import BenB. Variable P: B. Variable Q: B. Variable R: B. Theorem naam: (P -> Q) -> (Q -> R) -> P -> R. Proof. imp_i H1. imp_i H2. imp_i H3.
Bij de laatste stap ziet men in de bewijsboom van Coq dat aanname H1 overeenkomt met (P → Q), H2 met (Q → R), H3 met P en dat R te bewijzen is.
Coq voor propositielogica
Nadat een stelling als tautologie is opgeschreven kan men deze met Coq bewijzen door de commando's te gebruiken die bij de bewijsregels van de natuurlijke deductie horen. Het is echter ook mogelijk om een stelling automatisch te verifiëren. Hier enkele voorbeelden van deze mogelijkheden.
Het automatisch verifiëren van een correctheidsstelling in propositielogica
Coq kan een tautologie die enkel gebruik maakt van propositielogica automatisch bewijzen m.b.v. het commando tauto. Voor het werkstuk wordt het gebruik van deze regel niet geaccepteerd, maar het kan je helpen om snel stukken te bewijzen die je later nog eens zelf bewijst.
Bijvoorbeeld:
Require Import BenB. Variable P: B. Variable Q: B. Variable R: B. Goal (P -> Q) /\ (Q -> R) -> (P -> R). tauto. Qed.
Op het moment dat de stelling klopt, zal het volgende antwoord geven na het tauto commando:
Proof completed.
Is een stelling niet waar, dan geeft Coq het volgende antwoord:
Toplevel input, characters 1-6 > tauto. > ^^^^^ User error: Tauto failed
Echter, er zit wel een adder onder het gras. Omdat wij bij dit vak normaal gesproken eerst losse onderdelen specificeren en die vervolgens aan elkaar koppelen in een correctheidsstelling, betekent dat bijna automatisch dat we 'definities gaan gebruiken. Zie bijvoorbeeld de al eerder genoemde universele radio. (Merk op dat we nu Variables schrijven in plaats van Variable. Dat is simpelweg een afkorting om het mogelijk te maken om meerdere variabelen van hetzelfde type in één keer te declareren.)
Require Import BenB. Variables wissel110 wissel230 gelijk12: Prop. Variables ontvangst muziek: Prop. Definition ACDC := (wissel110 -> gelijk12) /\ (wissel230 -> gelijk12). Definition Radio := gelijk12 /\ ontvangst -> muziek. Definition GewensteEigenschap := (wissel110 \/ wissel230) /\ ontvangst -> muziek. Theorem OveralMuziek: ACDC /\ Radio -> GewensteEigenschap.
Als we nu direct het commando tauto proberen toe te passen, zal Coq zeggen dat die tactiek faalt. Vermoedelijk omdat het nu ACDC, Radio en GewensteEigenschap zelf als atomaire proposities opvat en dan is de stelling natuurlijk niet waar. Om dit probleem op te lossen, moet men eerst de definities uitvouwen via het commando unfold en pas daarna tauto gebruiken zoals hieronder voorgedaan.
Proof. unfold ACDC. unfold Radio. unfold GewensteEigenschap. tauto. Qed.
Natuurlijke deductie voor propositielogica: Voorbeeld 1
Hieronder een voorbeeld van een stelling in propositielogica en het Coq script om het te bewijzen.
Theorem naam: (P -> Q -> R) -> (P /\ Q -> R).
Het complete bewijs in Coq gaat als volgt:
Require Import BenB. Variable P: B. Variable Q: B. Variable R: B. Theorem naam: (P -> Q -> R) -> (P /\ Q -> R). Proof. imp_i H1. imp_i H2. imp_e Q. imp_e P. assumption. con_e1 Q. assumption. con_e2 P. assumption. Qed.
Natuurlijke deductie voor propositielogica: Voorbeeld 2
Nog een voorbeeld.
Require Import BenB. Variable p : B. Variable q : B. Variable r : B. Theorem th1 : p /\ (q \/ r) -> p /\ q \/ p /\ r. Proof. imp_i H1. dis_e (q \/ r) H2 H3. con_e2 p. assumption. dis_i1. con_i. con_e1 (q \/ r). assumption. assumption. dis_i2. con_i. con_e1 (q \/ r). assumption. assumption. Qed.
Coq voor predikaatlogica
Nadat een stelling als tautologie is opgeschreven kan men deze met Coq bewijzen door de commando's te gebruiken die bij de bewijsregels horen. De ∃I-regel wijkt in Coq een klein beetje af. Terwijl de regel op papier er niet om geeft welk speciaal geval je aanwijst, moet je er in Coq voor zorgen dat dit speciale geval ook daadwerkelijk bestaat. Nu is er soms niet altijd een geval beschikbaar. Het probleem zit hem er in dat de bewijsregels ervan uitgaan dat een domein (in dit geval D) niet leeg is, terwijl Coq daar niet van uitgaat. Je kunt Coq vertellen het domein tenminste 1 element bevat door te schrijven Variable c: D. je zegt daarmee dat in ieder geval c een onderdeel is van het domein D.
Natuurlijke deductie voor predikaatlogica: Voorbeeld 1
Een voorbeeld: het bewijs van ∀ x:D ⊢ ∃ x:D is prima te maken op papier, maar onmogelijk in Coq zonder een niet leeg domein aan te nemen! De Coq code voor dit bewijs is:
Require Import BenB. Variable D: Set. Variable c: D. Variable P: D -> Prop. Theorem th1: (forall x: D, P x) -> (exists x, P x). Proof. imp_i H1. exi_i c. all_e (forall x: D, P x) c. assumption. Qed.
Natuurlijke deductie voor predikaatlogica: Voorbeeld 2
Het bewijs van forall x:D, forall y:D, R x y -> ¬R y x ⊢ forall x:D, ¬R x x in Coq gaat als volgt:
Require Import BenB. Variable D : Set. Variable R : D -> D -> B. Theorem th1 : (forall x:D, forall y:D, R x y -> ~R y x) -> (forall x:D, ~R x x). Proof. imp_i H1. all_i a. neg_i (R a a) H2. imp_e (R a a). all_e (forall y:D, R a y -> ~R y a) a. all_e (forall x:D, forall y:D, R x y -> ~R y x) a. assumption. assumption. assumption. Qed.
Coq voor predikaatlogica met getallen, vergelijkingen en intervallen
Goede voorbeelden van de hier gebruikte constructies en commando's zijn te vinden op Beweren en bewijzen/het verhaal/6. Theorie/casus Drieminutenlicht en Beweren en bewijzen/het verhaal/6. Theorie/casus Iets met tijdsintervallen. In Beweren en Bewijzen gebruiken we twee soorten getallen die Coq ook kent: gehele getallen Z en reële getallen R. Alle gebruikelijke wiskundige operaties zijn voor beide soort aanwezig, alsmede notatie voor intervallen.
Commando reflexivity
Hoe bewijs je:
Theorem th1 : forall x : D, x = x.
Simpel weg met:
Proof. all_i a. reflexivity. Qed.
Commando replace
Hoe bewijs je:
Variable a:R. Variable b:R. Variable c:R. Theorem th1: (a=b -> b=c -> a=c).
Simpelweg met:
Proof. imp_i H1. imp_i H2. replace c with b. assumption. Qed.
In het algemeen vervangt replace t1 with t2 term t1 in de conclusie met de term t2. Een extra doel wordt dan om t2 = t1 te bewijzen. Als dit letterlijk in 1 van de aannames staat wordt automatisch assumption toegepast.
Een wat uitgebreider voorbeeld:
Require Import BenB. Definition T:=R. Variable P:T->B. Variable Q:T->B. Theorem hoofdstukVB : (forall t:T, P t -> Q (t+5)) -> (forall t:T, P (t-2) -> Q (t+3)). Proof. imp_i H1. all_i a. imp_i H2. replace (a+3) with (a-2+5). imp_e (P (a-2)). all_e (forall t:T, P t -> Q (t + 5)) (a-2). assumption. assumption. lin_solve. Qed.
Commando interval
Vouwt de definitie voor intervallen uit. Als er in de conclusie bijvoorbeeld staat:
t1 in [t2-3, t2)
Dan zorgt interval. voor:
t2 - 3 <= t1 /\ t1 < t2
Commando lin_solve
Lost een lineair stelsel van ongelijkheden op. Stel wat je bewijzen moet is: (zoals weergegeven in het Coq goal scherm, in feite staat er t2 ∈ (t1, t1 + 3] |- t2 - 5 <= t1)
H2: t2 in (t1, t1 + 3] ============================ t2 - 5 <= t1
Om lin_solve toe te kunnen passen, moeten we het eerst in een vorm schrijven waarbij de benodigde aannames simpele vergelijkingen zijn. Dat is hier nog niet het geval, omdat t2 in (t1, t1 + 3] in feite t1 < t2 /\ t2 <= t1 + 3 betekent en het dus een conjunctie van vergelijkingen is. Toepassen van imp_e (t2 <= t1+3). levert twee nieuwe doelen op.
Doel 1:
H2: t2 in (t1, t1 + 3] ============================ t2 <= t1 + 3
Dit lost men op met con_e2 (t1 < t2). gevolgd door assumption.
Doel 2:
H2: t2 in (t1, t1 + 3] ============================ t2 <= t1 + 3 -> t2 ─ 5 <= t1
Toepassen van imp_i H3. geeft het onderstaande. Merkop: het kan dus nodig zijn een implicatie eliminatie te doen direct gevolgd door een implicatie introductie!
H2: t2 in (t1, t1 + 3] H3: t2 <= t1 + 3 ============================ t2 ─ 5 <= t1
Uitvoeren van lin_solve. lost het in één keer op. Alle aannames worden automatisch in ogenschouw genomen.
Zoals gezegd kan lin_solve een stelsel ongelijkheden oplossen. Een voorbeeld van een ingewikkelder stelsel is het volgende doel met aannames:
H1: stoomduur - 5 < a H2: tijd + 5 < stoomduur ============================ tijd < a
Grote bewijzen
- Commando clear H1 laat aanname H1 verdwijnen. Dit kan helpen om het geheel overzichtelijker te maken.
- Commando unfold D ontvouwt de definitie D tot de kale formule overal in de conclusie.
- Commando unfold D in H ontvouwt de definitie D tot de kale formule overal in aanname H.
- In sommige situaties is het handig om Coq een beetje te helpen bij het bewijzen. Stellingen als
Theorem KleinerGelijkOfGroter: forall x:T, forall y:T, x<=y \/ y<x.
zijn waar als T bijvoorbeeld het domein van de reële getallen is, maar zijn heel lastig te bewijzen met de kennis van Coq zoals die bij dit vak wordt aangeleerd. Daarom is het toegestaan om in dit soort gevallen de speciale constructie Hypothesis te gebruiken.
Hypothesis KleinerGelijkOfGroter: forall x:T, forall y:T, x<=y \/ y<x.
Het grote verschil tussen een Theorem en een Hypothesis is dat een stelling eerst bewezen moet worden voordat hij verder in Coq gebruikt kan worden, terwijl zo'n hypothese gewoon altijd gebruikt kan worden. Het wordt simpelweg gezien als een extra aanname die niet expliciet in het lijstje aannames wordt getoond. Deze hypothese kan op twee manieren gebruikt worden: met hyp en met apply. Hieronder een paar voorbeelden waarin het verschil blijkt:
Require Import BenB. Definition T:=R. Hypothesis KleinerGelijkOfGroter: forall x:T, forall y:T, x<=y \/ y<x. Theorem Waar: 5 <= 7 \/ 7 < 5. Proof. dis_i1. lin_solve. Qed. Theorem OokWaarViaApply: forall x:T, 5 <= (7 + x) \/ (7 + x) < 5. Proof. all_i x1. apply KleinerGelijkOfGroter. Qed. Theorem OokWaarViaHyp: forall x:T, 5 <= (7 + x) \/ (7 + x) < 5. Proof. all_i x1. all_e (forall y:T, 5 <= y \/ y < 5) (7+x1). all_e (forall x:T, forall y:T, x<=y \/ y<x) 5. hyp KleinerGelijkOfGroter. Qed. Theorem VerkeerdOmMaarOokWaar: forall x:T, (7 + x) < 5 \/ 5 <= (7+x). Proof. all_i x1. imp_e (5 <= (7+x1) \/ (7+x1) < 5). imp_i a1. dis_e (5 <= 7 + x1 \/ 7 + x1 < 5) a2 a3. hyp a1. dis_i2. hyp a2. dis_i1. hyp a3. apply KleinerGelijkOfGroter. Qed.
In deze hypothese staan kwantoren. Als we hyp KleinerGelijkOfGroter willen gebruiken, moeten we er natuurlijk ook voor zorgen dat er exact die hypothese staat. Als we apply gebruiken, gaat Coq zelf kijken of hij instanties van de ∀ x en ∀ y kan vinden zodat de hypothese precies past bij de stelling.
- Toevallig heeft deze hypothese geen aannames. Dat kan echter ook. Na het toepassen van zo'n hypothese met aannames zal Coq dan ook precies de aannames van de hypothese als nieuwe bewijsverplichting opveoren.
- Omdat Hypothesis dus als een onzichtbare aanname wordt gebruikt, kan het soms handig zijn om Hypothesis te gebruiken in plaats van Definition. De bewijsboom wordt daardoor kleiner en dus sneller te genereren door Coq.
- Diezelfde
applykan ook gebruikt worden met hulptheorema's. Zie het onderstaande voorbeeld waarin hulptheoremath3is gemaakt, die met behulp vanapply th3in het bewijs van theoremath4wordt gebruikt. Merkop dat de gekwanticifeerde variabelexvanzelf goed wordt ingevuld mett. N.b. in de Fitch-view wordt niet aangegeven wanneer welk hulptheorema wordt gebruikt. Dit zul je er dus zelf bij moeten zetten.
Require Import BenB. Theorem th3 : forall x:R, x<3 -> x<5. Proof. all_i x. imp_i H1. lin_solve. Qed. Variable t : R. Theorem th4 : (t in [0,3) -> t in [0,5)). Proof. imp_i H1. interval. con_i. con_e1 (t<3). assumption. imp_e (t<3). apply th3. con_e2 (0<=t). assumption. Qed.
Werken met eindige verzamelingen in Coq
Bij veel werkstukken is er de behoefte om 'labels', constanten of zogenaamde enumeratie types te kunnen gebruiken. Bijvoorbeeld om de verschillende kleuren rood, geel en groen van een verkeerslicht expliciet in een predikaat te kunnen gebruiken. Of juist om de posities links, rechts, boven en onder te kunnen onderscheiden. Dit kan relatief eenvoudig in Coq en wel op de volgende manier:
Inductive Lampkleuren : Set := rood | geel | groen.
Dit heeft precies de gewenste eigenschappen:
- Er zijn drie verschillende lampkleuren.
- Er zijn geen andere kleuren dan rood, geel en groen.
Beide eigenschappen kunnen we zelfs bewijzen in Coq, al hebben we daar wel een paar commando's voor nodig die wij normaal gesproken niet gebruiken binnen deze cursus.
Theorem AlleKleurenZijnVerschillend: ~(rood = geel) /\ ~(geel = groen) /\ ~(groen = rood). Proof. con_i. discriminate. con_i. discriminate. discriminate. Qed. Theorem AllesIsRoodGeelOfGroen: forall lk:Lampkleuren, lk = rood \/ lk = geel \/ lk = groen. Proof. all_i lampkleur. case lampkleur. dis_i1. lin_solve. dis_i2. dis_i1. lin_solve. dis_i2. dis_i2. lin_solve. Qed.
Deze constanten kunnen we nu gebruiken om bijvoorbeeld drie instanties van een tamelijk triviale lamp te maken. En die lampen kunnen dan weer gecombineerd worden tot een verkeerslicht.
Definition T:=R. Variable krijgtStroom: T -> Lampkleuren -> B. Variable geeftLicht: T -> Lampkleuren -> B. Definition Lamp (lk:Lampkleuren) := forall t:T, krijgtStroom t lk -> geeftLicht t lk. Definition Verkeerslicht := Lamp rood /\ Lamp geel /\ Lamp groen /\ forall t:T, krijgtStroom t rood \/ krijgtStroom t geel \/ krijgtStroom t groen.
En hiermee kan natuurlijk ook weer bewezen worden dat zo'n verkeerslicht altijd een of andere kleur licht geeft.
Theorem AltijdLicht: Verkeerslicht -> forall t:T, exists lk:Lampkleuren, geeftLicht t lk. Proof. imp_i vkl. all_i t0. unfold Verkeerslicht in vkl. dis_e ( krijgtStroom t0 rood \/ krijgtStroom t0 geel \/ krijgtStroom t0 groen) ro gegr. all_e (forall t : T, krijgtStroom t rood \/ krijgtStroom t geel \/ krijgtStroom t groen) t0. con_e2 (Lamp groen). con_e2 (Lamp geel). con_e2 (Lamp rood). assumption. exi_i rood. unfold Lamp in vkl. imp_e (krijgtStroom t0 rood). all_e (forall t : T, krijgtStroom t rood -> geeftLicht t rood) t0. con_e1 (Lamp geel /\ Lamp groen /\ (forall t : T, krijgtStroom t rood \/ krijgtStroom t geel \/ krijgtStroom t groen)). assumption. assumption. dis_e (krijgtStroom t0 geel \/ krijgtStroom t0 groen) gee gro. assumption. exi_i geel. imp_e (krijgtStroom t0 geel). all_e (forall t : T, krijgtStroom t geel -> geeftLicht t geel) t0. con_e1 (Lamp groen /\ (forall t : T, krijgtStroom t rood \/ krijgtStroom t geel \/ krijgtStroom t groen)). con_e2 (Lamp rood). assumption. assumption. exi_i groen. imp_e (krijgtStroom t0 groen). all_e (forall t : T, krijgtStroom t groen -> geeftLicht t groen) t0. con_e1 (forall t : T, krijgtStroom t rood \/ krijgtStroom t geel \/ krijgtStroom t groen). con_e2 (Lamp geel). con_e2 (Lamp rood). assumption. assumption. Qed.
Coq in Mac OS X
Als je Coq hebt gedownload voor je Mac, is het wat werk om het programma en de B&B import aan de gang te krijgen. Je zult de compiler naar de juiste directory moeten wijzen om BenB.v te kunnen vinden.
Download BenB.v (de link bevindt zich bovenaan deze pagina) en plaats het in een directory. Ik koos voor Documents/BenB.
De voorbeelden in deze wiki beginnen doorgaans zo:
Require Import BenB.
Voor de Mac veranderen we dat naar:
Add LoadPath "/Users/sander/Documents/BenB". Require Import BenB.
Uiteraard verander je je de directory naar die waar jij je bestand hebt neergezet. Door "Add LoadPath" uit te voeren voeg je de directory waar BenB.v staat toe aan het LoadPath (daar waar Coq óók zoekt naar bestanden).
Mocht Coq dan alsnog klagen over een ontbrekende library, dan moet je BenB.v handmatig compilen. Open het bestand in CoqIde en klik in het menu Compile' op Make. Dit maakt de BenB.glo en BenB.vo die direct te importeren zijn.